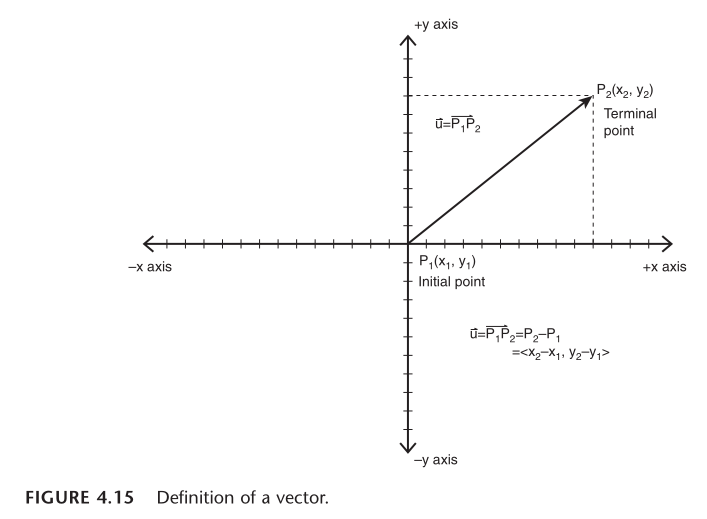
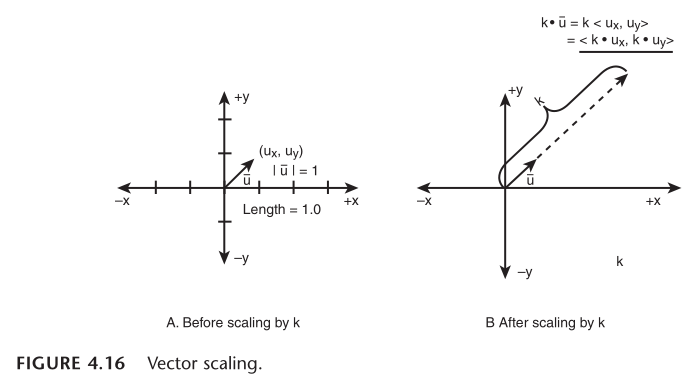
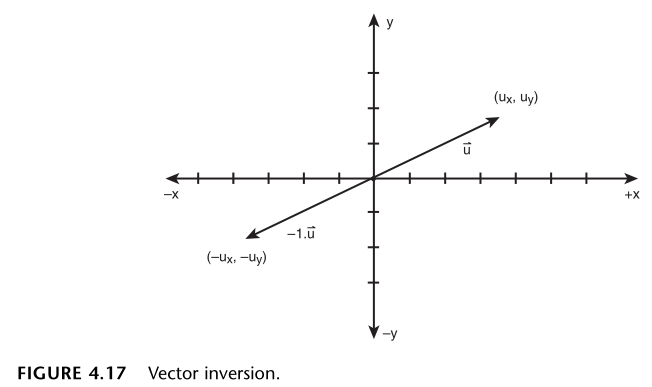
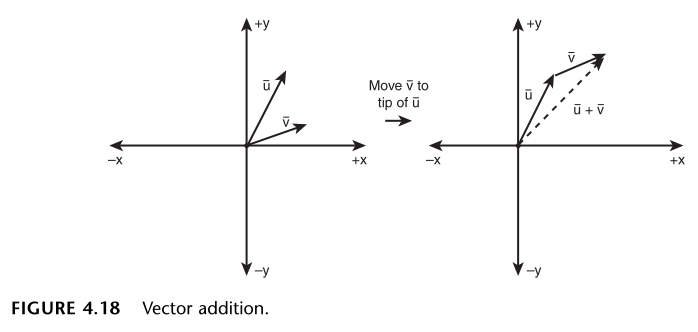
最近在学习《3D 游戏编程大师技巧》第 4 章,摘抄一些我认为重要的信息,并添加上自己的一些思考。
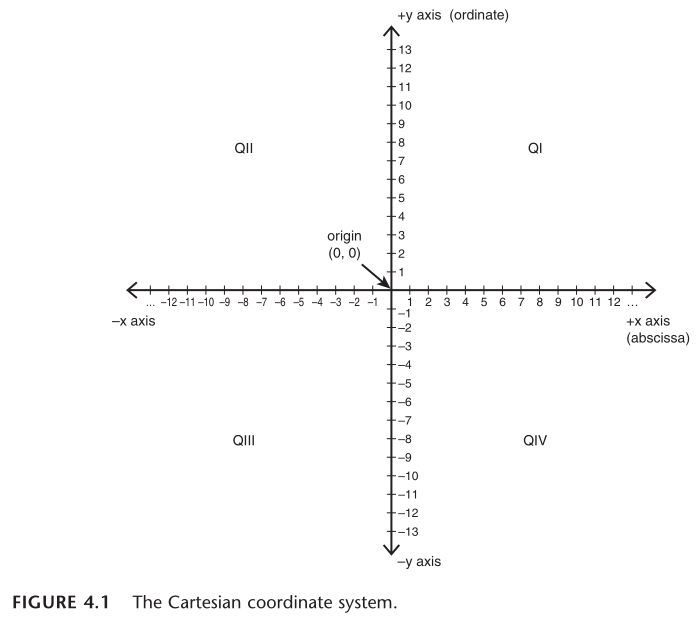
提示:很多图形算法都以这样的方式进行优化:首先在 Q1 中解决问题,然后根据对称性将解决方案反射到其它象限(在 3D 坐标系中为卦限)。
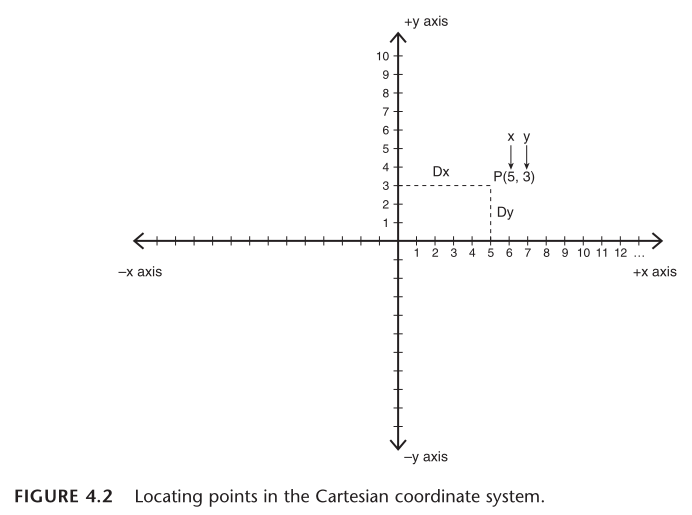
另一种支持两个自由度的坐标系是极坐标(polar coordinates)系。极坐标是游戏 Wolfenstein 和光线投射技术的基础。极坐标使用方向(heading)和距离来定义 2D 空间中的点,而不是使用 (x, y) 坐标。
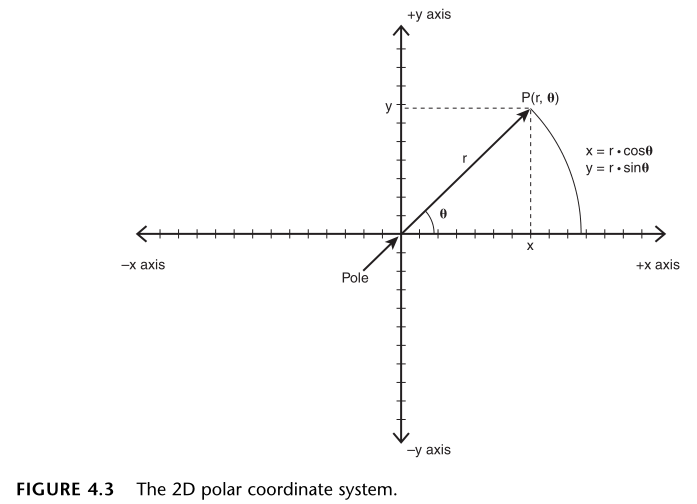
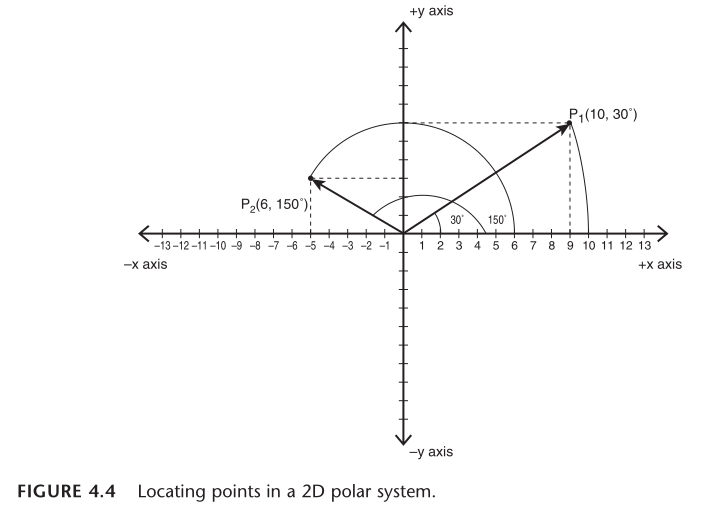
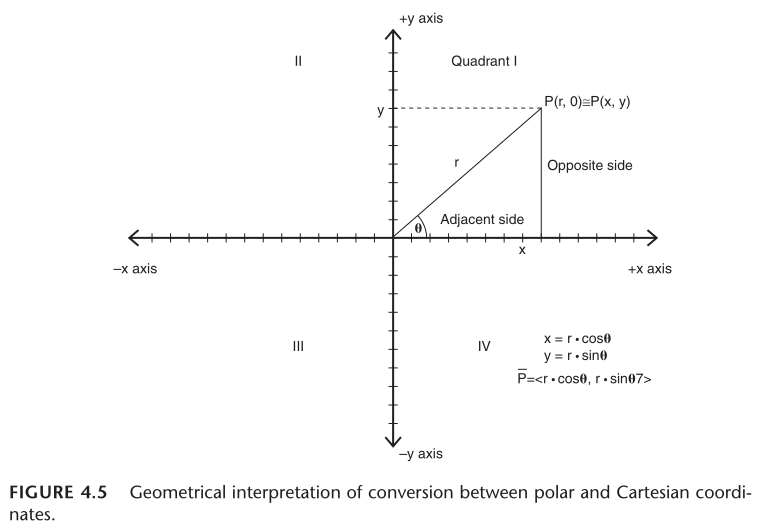
极坐标 (r, θ) 转为笛卡尔坐标 (x, y):
- x = r * cosθ
- y = r * sinθ
笛卡尔坐标 (x, y) 转为极坐标 (r, θ):
- r = sqrt(x2 + y2)
- θ = tan-1(y/x) (注意 y/x 时必须 x ≠ 0)
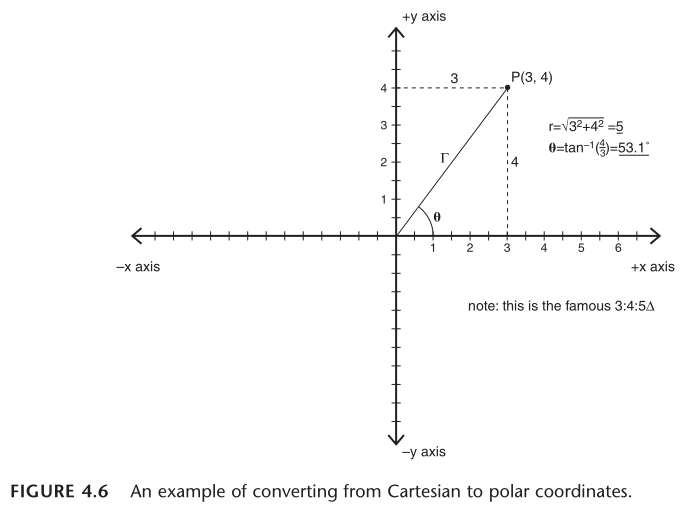
极坐标很有用,理解极坐标以及如何进行坐标变换对于解决很多有关弹道、瞄准和导航的问题非常重要。
如果您人事过游戏编程,可能熟悉 3D 坐标系。但这里还是要介绍一下柱面坐标系和球面坐标系,因为它们对实现纹理映射和其它特殊效果很有帮助。
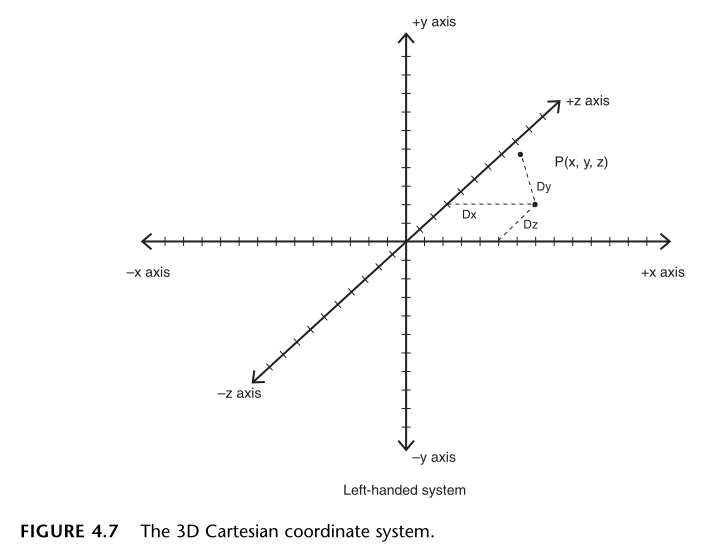
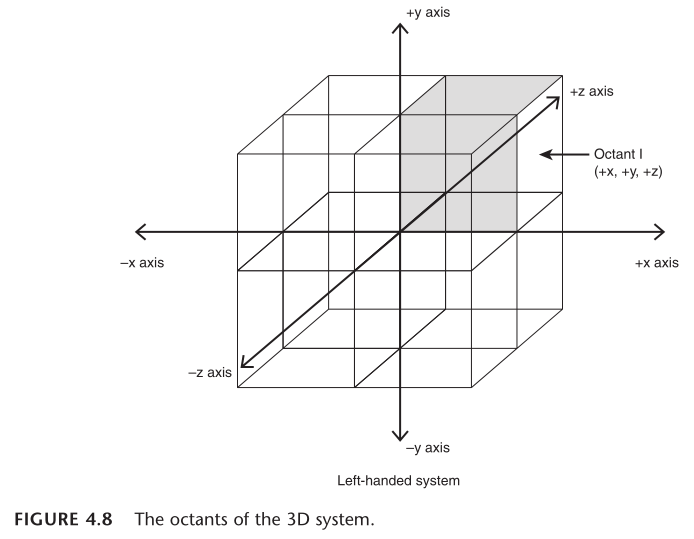
(3D 笛卡尔坐标系)新增的 z 轴带来了一个小问题,必须决定在两个不同的方向中,哪个代表 z 轴的正半空间,哪个代表 z 轴的负半空间。因此,有两种不同的 3D 笛卡尔坐标系:左手坐标系和右手坐标系。
在标准的 2D 笛卡尔坐标系中(图 4.1):
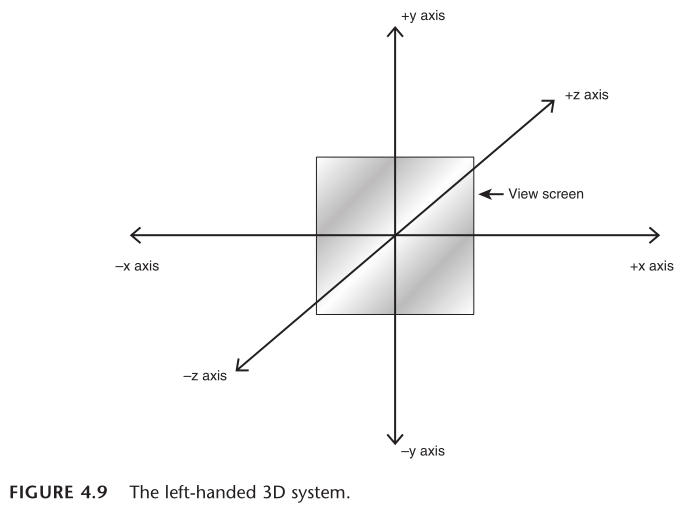
- 如果新增的 z 轴正方向指向屏幕内,则是左手坐标系(图 4.9)
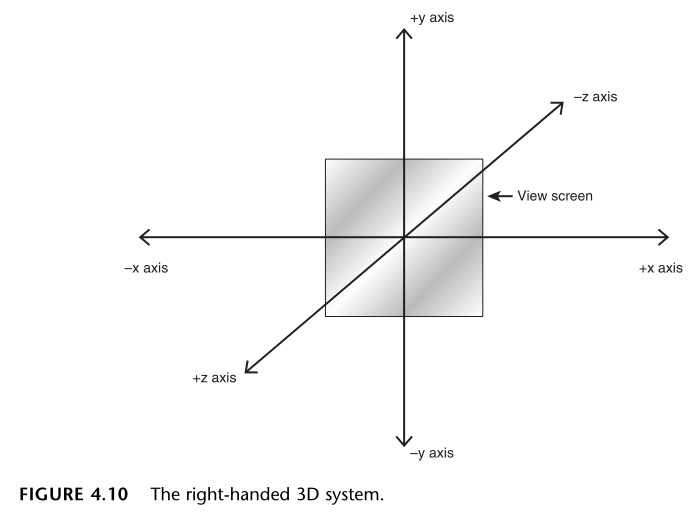
- 如果新增的 z 轴正方向指向屏幕外,则是右手坐标系(图 4.10)
3D 柱面坐标系最接近于 2D 极坐标系,因为它只是在 2D 极坐标系的基础上增加了一条 z 轴,如图 4.11。
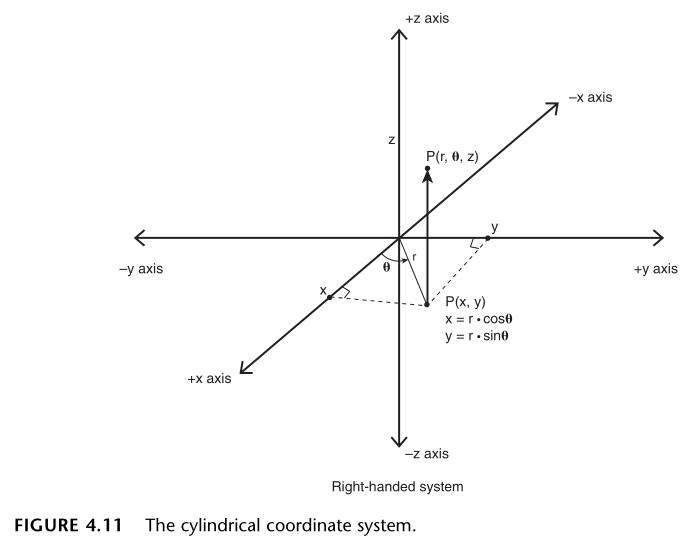
我的理解是,3D 柱面坐标系中的 x-y 平面使用的极坐标形成一个圆,再加上 z 轴就形成一个圆柱体了。
3D 柱面坐标 (r, θ, z) 转为 3D 笛卡尔坐标 (x, y, z):
- x = r * cosθ
- y = r * sinθ
- z = z
3D 笛卡尔坐标 (x, y, z) 转为 3D 柱面坐标 (r, θ, z):
- r = sqrt(x2 + y2)
- θ = tan-1(y/x) (注意 y/x 时必须 x ≠ 0)
- z = z
对于很多问题,使用柱面坐标是非常方便的,如在第一人称射击游戏中控制相机、环境映射等。
假设 P 点在三维空间的位置的球面坐标是 (r, φ, θ),那么:
- r 是从原点到 P 点的距离
- φ 是从原点到 P 点的线段,在 x-y 平面的投影线,与 +x 轴的夹角
- θ 是从原点到 P 点的线段,与 +z 轴的夹角
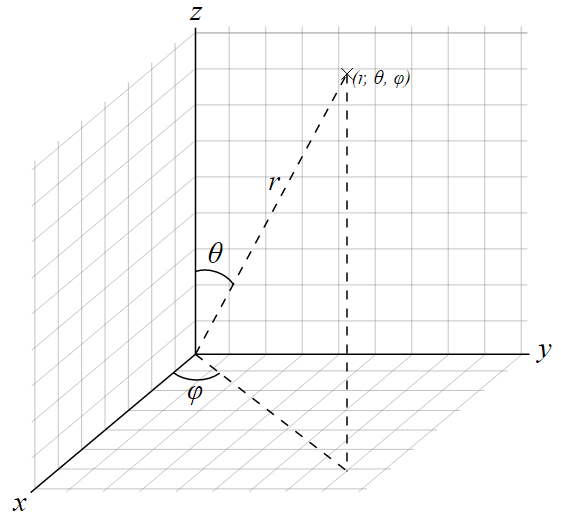
我的疑问:使用球面坐标系的好处是什么?在什么情况下会比 3D 笛卡尔/柱面坐标系方便?
球面坐标 (r, φ, θ) 转为 3D 笛卡尔坐标 (x, y, z):
- x = r * sinθ * cosφ
- y = r * sinθ * sinφ
- z = r * cosθ
3D 笛卡尔坐标 (x, y, z) 转为球面坐标 (r, φ, θ):
- r = sqrt(x2 + y2 + z2)
- φ = tan-1(y / x)
- θ = cos-1(z / r)
- θ = sin-1(p / r) (p 为从原点到 P 点的线段,在 x-y 平面的投影线的长度,即 sqrt(x2 + y2))


注意:在计算机上,无法表示无穷大,但在这种环境下,无穷大指的是这样的数字,即它们足够大,比我们考虑的数字空间中的任何数还要大很多倍。例如,如果游戏空间为 1000 * 1000 的网格,则可以认为 100,000,000 接近无穷大。
下面列出常用的一些三角恒等式。
倒数函数:
- 正割:csc(θ) = 1 / sin(θ)
- 余割:sec(θ) = 1 / cos(θ)
- 余切:cot(θ) = 1 / tan(θ)
勾股定理的三角函数表示:
- sin(θ)2 + cos(θ)2 = 1
转换恒等式:
- sin(θ) = cos(θ – PI/2)
反射恒等式:
- sin(-θ) = -sin(θ)
- cos(-θ) = cos(θ)
角度相加恒等式:
- sin(θ1 + θ2) = sin(θ1) * cos(θ2) + cos(θ1) * sin(θ2)
- cos(θ1 + θ2) = cos(θ1) * cos(θ2) - sin(θ1) * sin(θ2)
- sin(θ1 - θ2) = sin(θ1) * cos(θ2) - cos(θ1) * sin(θ2)
- cos(θ1 - θ2) = cos(θ1) * cos(θ2) + sin(θ1) * sin(θ2)
技巧:后面讨论矩阵变换时,可能将多种操作(如平移、旋转、缩放等)组合起来。旋转操作本身可能是多个用正弦和余弦表示的旋转变换的组合。因此,计算矩阵乘法时,可以使用三角恒等式来简化矩阵,编写一个具体的函数来执行变换操作,而不是盲目地使用通用的矩阵乘法。