At the core, we require ways to represent basic data types, such as approximations to integer and real arithmetic. From there we can consider how machine-level instructions manipulate data and how a compiler translates C programs into these instructions.

Modern computers store and process information represented as 2-valued signals. These lowly binary digits, or bits, form the basis of the digital revolution.

信息存储

In isolation, a single bit is not very useful. When we group bits together and apply some interpretation that gives meaning to the different possible bit patterns, however, we can represent the elements of any finite set.

现代计算机保存和处理的信息，其实都是一组 01 电信号。显然，单个电信号位只能表示两个值，用处不大，组合多个电信号，每种组合表示一种信息。对于多种组合，对其进行不同的解析（interpretation），可以表示多种不同的信息。

数据在计算机中都以二进制 01 串表示，不同的编码（encoding）能表示不同类型的数据，不同的解析方式（interpretation）读取不同类型的数据，如整数、浮点数、字符、字符串、可执行文件等。

Computer representations use a limited number of bits to encode a number and hence some operations can overflow when the results are too large to be represented.

对于 32 位设备，总共可以表示 2³² 种信息。但如果信息总量超过了 2³² 种，则 32 位设备无法一一对应表示这么多信息，就会溢出（overflow）。

注：为了方便阐述，以下默认机器都是 32 位。

Floating-point arithmetic is not associative, due to the finite precision of the representation. For example, the C expression (3.14+1e20)-1e20 will evaluate to 0.0 on most machines, while 3.14+(1e20-1e20) will evaluate to 3.14. The different mathematical properties of integer vs. floating-point arithmetic stem from the difference in how they handle the finiteness of their representations - integer representations can encode a comparatively small range of values, but do so precisely, while floating-point representations can encode a wide range of values, but only approximately.

Q：如何表示浮点数？比如一个浮点数占 4 字节，那么 2 字节表示整数，2 字节表示小数吗？

Rather than accessing individual bits in memory, most computers use blocks of eight bits, or bytes, as the smallest addressable unit of memory. A machine-level program views memory as a very large array of bytes, referred to as virtual memory. Every byte of memory is identified by a unique number, known as its address, and the set of all possible addresses is known as the virtual address space.

大多数计算机使用 8 位二进制组合而成的字节（byte）来表示一块信息，并作为最小的可寻址单位，即存储器每个地址表示的数据都是一个字节，而不是一个位。具象地理解，就像街上每间店铺都有一个门牌号，店铺 = 每个字节，门牌号 = 每个字节对应的虚拟地址。

In subsequent chapters, we will cover how the compiler and run-time system partitions this memory space into more manageable units to store the different program objects, that is, program data, instructions, and control information. Various mechanisms are used to allocate and manage the storage for different parts of the program. This management is all performed within the virtual address space.

Although the C compiler maintains pointer type information, the actual machine-level program it generates has no information about data types. It simply treats each program object as a block of bytes, and the program itself as a sequence of bytes.

十六进制表示法

由于二进制表示过于冗长，所以使用十六进制来表示。每个十六进制位，能表示 4 个二进制位的所有组合（16 = 2⁴）。两个十六进制位能表示一个字节。

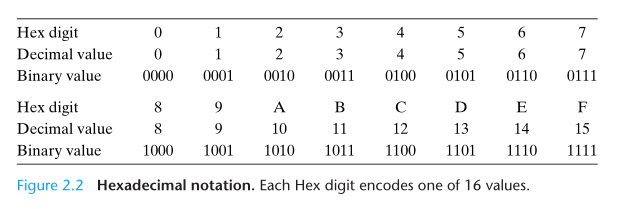
Every computer has a word size, indicating the nominal size of integer and pointer data. Since a virtual address is encoded by such a word, the most important system parameter determined by the word size is the maximum size of the virtual address space. That is, for a machine with a w-bit word size, the virtual addresses can range from 0 to 2^w-1, giving the program access to at most 2^w bytes.

字

计算机的字长（word-size），表示单个整数或指针数据所占内存大小。

我对 word 的理解是，操作系统对内存的解析（interpret）和使用的最小单位。比如在 32 位设备上，一个 word 就是 32 位，设备能访问的虚拟地址的范围是 0 到 2³²-1。

数据大小

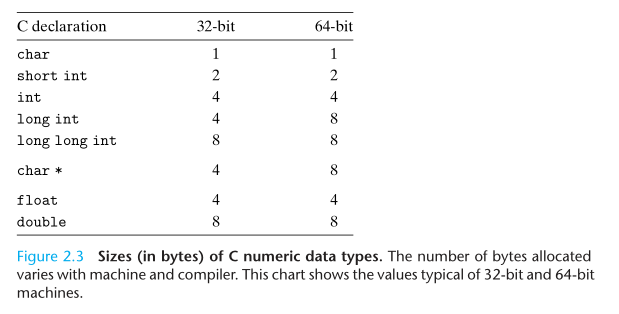
A “long” integer uses the full word size of the machine. A pointer also uses the full word size of the machine.

One aspect of program portability is to make the program insensitive to the exact sizes of the different data types.

寻址和字节序

For program objects that span multiple bytes, we must establish two conventions: what the address of the object will be, and how we will order the bytes in memory (Big endian / Little endian).

对于多字节对象，不同设备可能使用不同的字节排列方式，Big endian 是最高有效字节排在前面，Little endian 是最高有效字节排在后面。

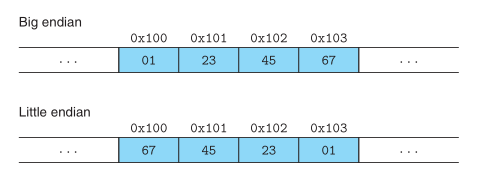
For most application programmers, the byte ordering used by their machines are totally invisible; programs compiled for either class of machine give identical results. At times, however, byte ordering becomes an issue. The first is when binary data are communicated over a network between different machines. A common problem is for data produced by a little-endian machine to be sent to a big-endian machine, or vice verse, leading to the bytes within the words being in reverse order for the receiving program. To avoid such problems, code written for networking applications must follow established conventions for byte ordering to make sure the sending machine converts its internal representation to the network standard, while the receiving machine converts the network standard to its internal representation.

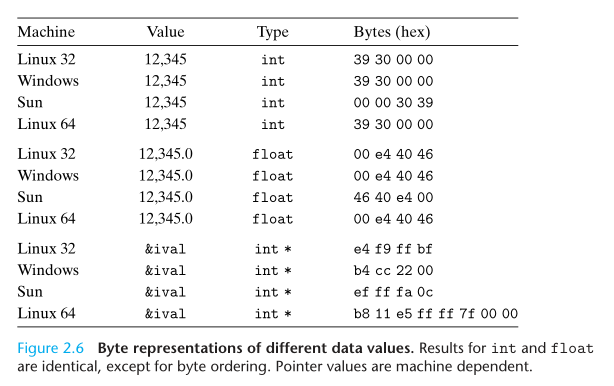
A second case where byte ordering becomes important is when looking at the byte sequences representating integer data. This occurs often when inspecting machine-level programs.

The disassembler is a tool that determines the instruction sequence represented by an executable program file. It is a program that converts an executable program file back to a more readable ASCII form.

A third case where byte ordering becomes visible is when programs are written that circumvent the normal type system.

字符串表示

This same result would be obtained on any system using ASCII as its character code, independent of the byte ordering and word size conventions. As a consequence, text data is more platform-independent than binary data.

字符串其实也是一堆 01 数据，对其使用不同的字符编码集（如 ASCII，Unicode 等），能解析出不同的字符。

代码表示

Different machine types use different and incompatible instructions and encodings. Even identical processors running different operating systems have differences in their coding conventions and hence are not binary compatible. Binary code is seldom portable across different combinations of machine and operating system.

A fundamental concept of computer systems is that a program, from the perspective of the machine, is simply a sequence of bytes. The machine has no information about the original source program, except perhaps some auxiliary tables maintained to aid in debugging.

Q：对于同一份二进制数据，是不是有类型信息？否则系统如何知道有什么方式解析这些数据？

布尔代数

布尔代数有：

按位与 &
按位或 |
按位异或 ^

C 语言的逻辑操作

按值与 &&
按值或 ||
按值异或 ^

C 语言中移位操作

对于布尔代数来说，向量 a 的加法逆元是 a 本身，运算是异或运算，即 a ^ a = 0，这里的 0 是指全为 0 的位向量。

位运算的一个常用用法是掩码（masking）操作。

Computers generate color pictures on a video screen or liquid crystal display by mixing three different colors of light: red, green and blue.

One common use of bit-level operations is to implement masking operations, where a mask is a bit pattern that indicates a selected set of bits within a word. As example, the mask 0xFF (having ones for the least significant 8 bits) indicates the low-order byte of a word. The expression ~0 will yield a mask of all ones, regardless of the word size of the machine. Although the same mask can be written 0xFFFFFFFF for a 32-bit machine, such code is not as portable.

a & (b | c) = (a & b) | (a & c)
a | (b & c) = (a | b) & (a | c)
a ^ a = 0
a ^ b = (a & ~b) | (~a & b)

A logical right shift fills the left end with k zeros, giving a result [0, …, 0, x_n-1, x_n-2, …, x_k]. An arithmetic right shift fills the left end with k repetitions of the most significant bit, giving a result [x_n-1, …, x_n-1, x_n-1, x_n-2, …, x_k].

C 语言提供移位运算，分别为：

<< 左移位后，在低位补 0。
>> 逻辑右移，在高位补 0。
>> 算术右移，在高位补原最高位的值。

如果对于 w 位数据，移 k > w 位怎么办？一般做法是移动 k mod w 位。

The C standard do not precisely define which type of right shift should be used. For unsigned data (i.e., integral objects declared with the qualifier unsigned), right shifts must be logical. For signed data (the default), either arithmetic or logical shifts may be used. This unfortunately means that any code assuming one form or the other will potentially encounter portability problems. In practice, however, almost all compiler/machine combinations use arithmetic right shifts for signed data, and many programmers assume this to be the case.

Java, on the other hand, has a precise definition of how right shifts should be performed. The expression x >> k shifts x arithmetically by k positions, while x >>> k shifts it logically.

整数表示

对于数的表示，可分为无符号数（unsigned numbers）和有符号数（signed numbers）。

对于无符号整数（unsigned integers），其二进制 01 串里每一位都是数位。
对于有符号整数（signed integers），其二进制 01 串里，最高位是符号位，其它的是数位。
- 有符号数共有三种表示法：补码（Two’s Complement）／反码（Ones’ Complement）／原码（Sign-Magnitude）。

同一个数字的整数和浮点数的二进制表示里，有若干相同的数位。在后面学习的浮点数表示会了解到原因。

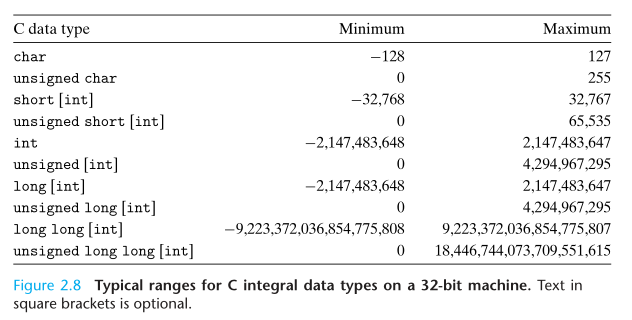
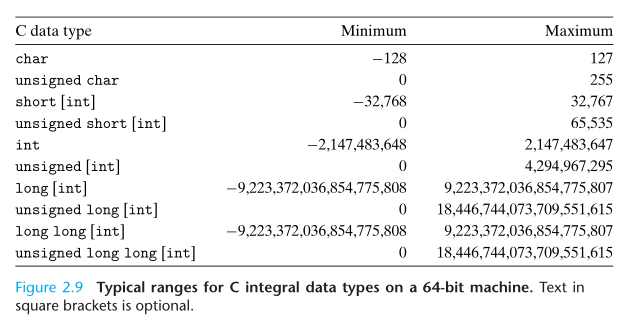
整数的数据类型

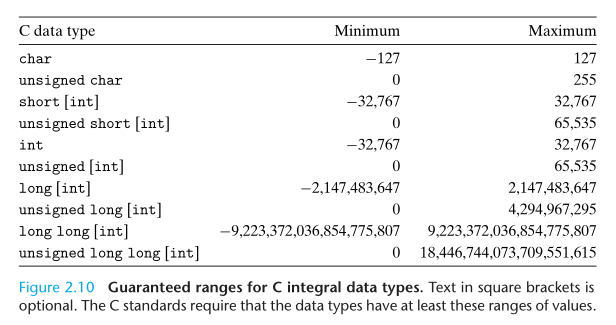
无符号整数编码

Both C and C++ support signed (the default) and unsigned numbers. Java supports only signed numbers.

对于无符号整数，二进制转换到十进制的方法，见公式 2.1：

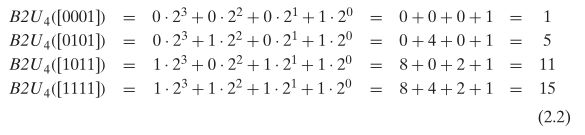
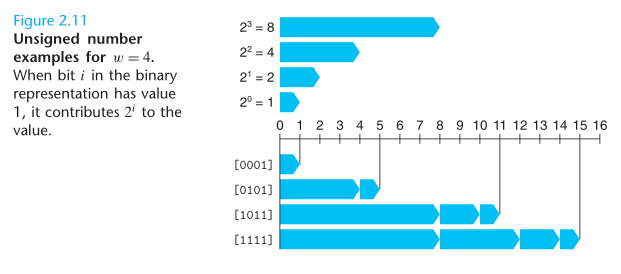
The most common computer representation of signed numbers is known as two’s-complement form. This is defined by interpreting the most significant bit of the word to have negative weight.

有符号整数的补码编码

对于有符号整数，一般使用补码表示，最高位表示负权（negative weight）。比如一个 32 位数据，最高位的负权就是 -1 * x₃₁ * 2³¹。二进制转换到十进制的方法，见公式 2.3：

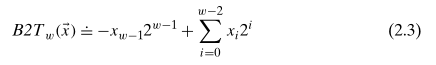
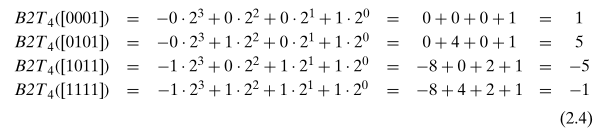
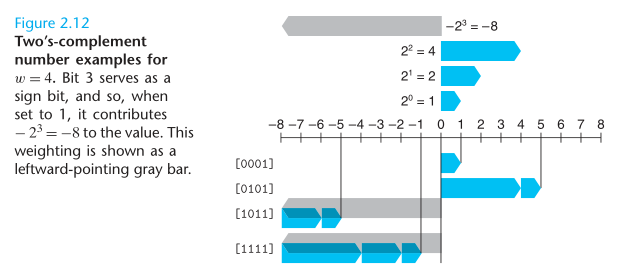
我对 B2T_w 公式的理解是，要计算 -x 的二进制序列，使用 -x + x = 0 来反推，而不是使用二进制序列最高位仅作为符号，后面各位之和作为值。

另外，有一点非常值得我们注意，就是有符号整数的取值范围，以 32 位为例，是 [1000 0000 0000 0000 0000 0000 0000 000, 0111 1111 1111 1111 1111 1111 1111 1111]，即 [0x8000 0000, 0x7FFF FFFF]，即 [-2³¹, 2³¹ - 1]。我们把 TMin₃₂ 定义为 -2³¹，TMax₃₂ 定义为 2³¹ - 1，那么 |TMin₃₂| = |TMax₃₂| + 1。TMin 没有与其相对应的正数，所以 TMin 的值会表示为 -TMax - 1。

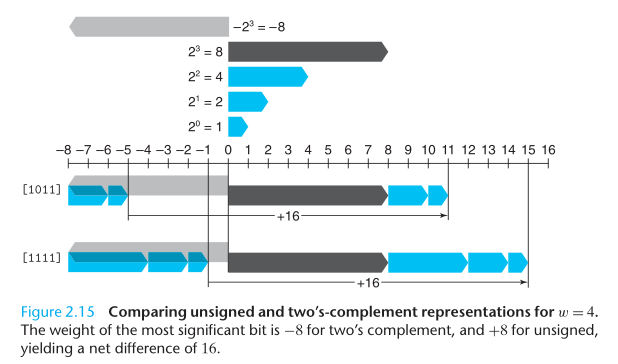
We see that the bit patterns are identical for Figures 2.11 and 2.12 (as well as for Equations B2U_w and B2T_w), but the values differ when the most significant bit is 1, since in one case it has weight +8, and in the other case it has weight -8.

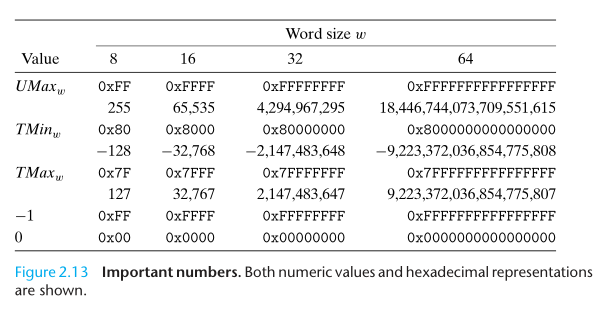
The ISO C99 standard introduces another class of integer types in the file stdint.h. This file defines a set of data types with declarations of the form intN_t and uintN_t, specifying N-bit signed and unsigned integers, for different values of N. The exact values of N are implementation dependent, but most compilers allow values of 8, 16, 32, and 64. Thus, we can unambiguously declare an unsigned, 16-bit variable by giving it type uint16_t, and a signed variable of 32 bits as int32_t.
Along with these data types are a set of macros defining the minimum and maximum values for each value of N. These have names of the form INITN_MIN, INTN_MAX, and UINTN_MAX.

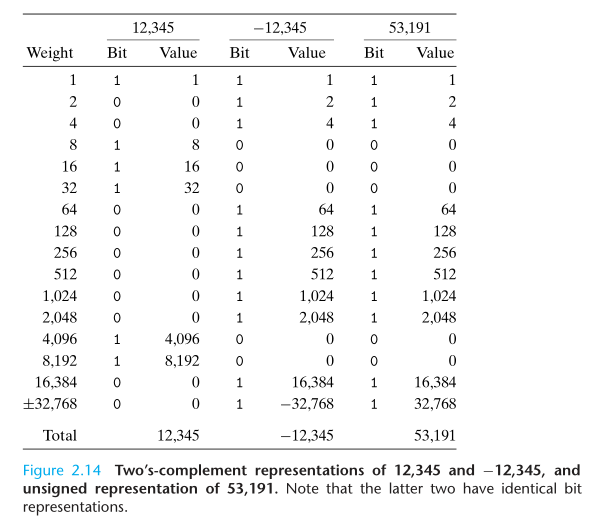
有符号/无符号整数之间的转换

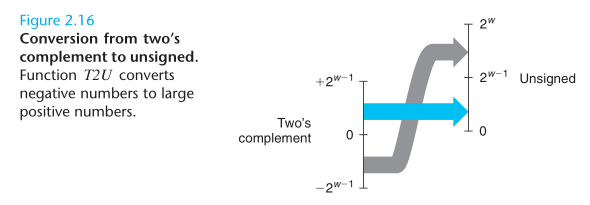
The effect of converting in both directions between unsigned and two’s complement representations, is to keep the bit patterns identical but change how these bits are interpreted.

对于无符号整数和有符号整数之间的转换，采取的原则是：保持原二进制表示不变，使用不同的解析方式来解析。对于同一个二进制表示对应的无符号整数 U 和有符号整数补码 T 之间的关系（以 32 位为例，且 T 为负数），则是 T = U - 2 * 2³¹ = U - 2³²，因为最高位的权从无符号的 2³¹ 变为有符号的 -2³¹，即公式 2.6。

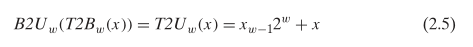
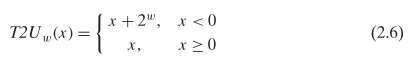
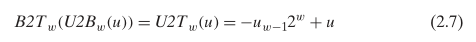
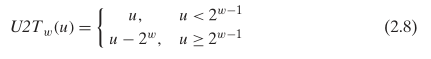
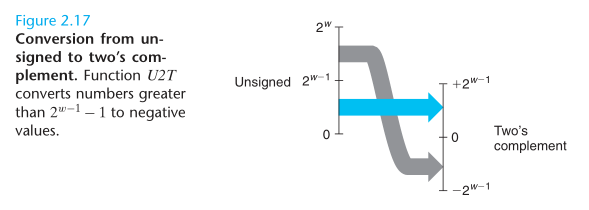
C 语言中的有符号/符号整数

When an operation is performed where one operand is signed and the other is unsigned, C implicitly casts the signed argument to unsigned and performs the operations assuming the numbers are nonnegative.

扩展一个数字的位表示

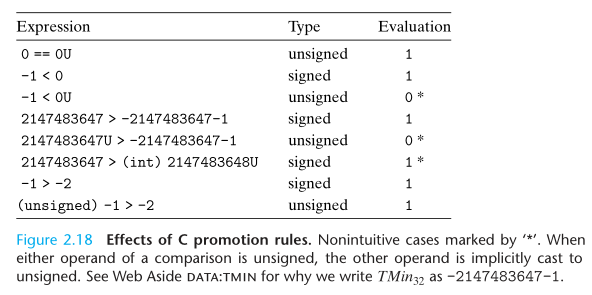
To convert an unsigned number to a larger data type, we can simply add leading zeros to the representation; this operation is known as zero extension. For converting a two’s complement number to a larger data type, the rule is to perform a sign extension, adding copies of the most significant big to the representation. Thus, if our original value has bit representation [x_w-1, …, x_w-1, x_w-1, x_w-2, …, x₀].

关于扩展数位（不能改变原来的值）：

无符号整数扩展数位，在高位补 0，这样不会改变原来的值。
有符号整数扩展数位，在高位补原最高位的值。对于负数在高位补 1 不会改变原来的值，见下面的数学归纳法证明。

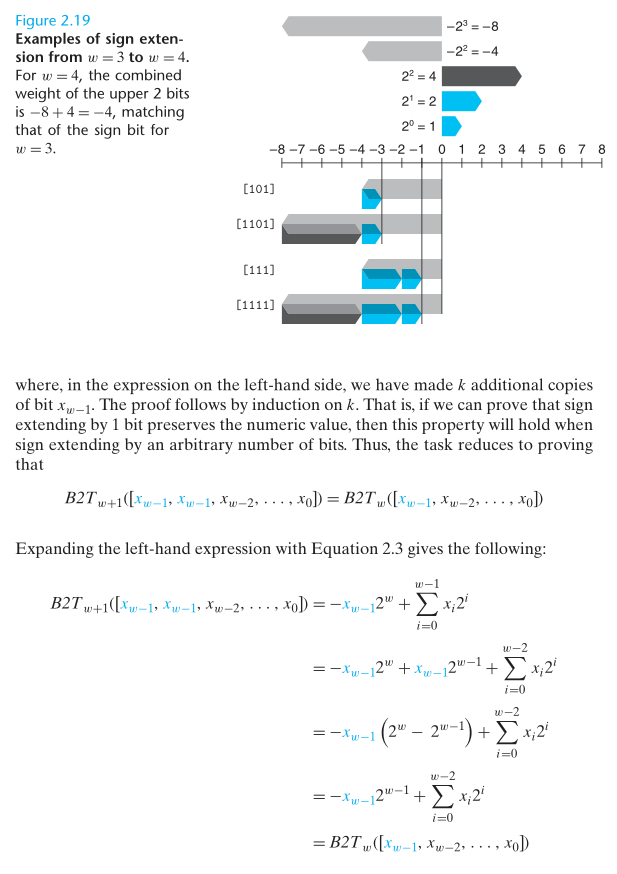
截断数字

关于减少数位，丢弃高 w-k 位，截断一个数字可能会改变其值。

对于无符号数 x，截断到 k 位后的值为 x mod 2^k，因为 w-k 位所表示的值能被 2^k 整除。
对于有符号数的补码表示，截断到 k 位后的值为 U2T_w(x mod 2^k)。

When truncating a w-bit number x = [x_w-1, x_w-2, …, x₀] to a k-bit number, we drop the high-order w-k bits, giving a bit vector x’ = [x_k-1, x_k-2, …, x₀]. Truncating a number can alter its value - a form of overflow. For an unsigned number x, the result of truncating it to k bits is equivalent to computing x mod 2^k.

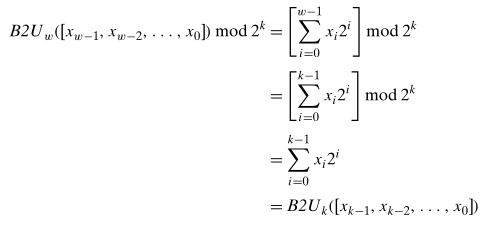
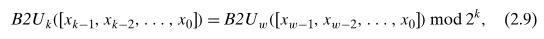
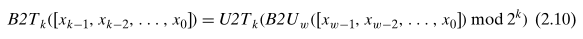
We can see that this problem arises due to the mismatch between data types: in one place the length parameter is signed; in another place it is unsigned. Such mismatches can be a source of bugs and ,at this example shows, can even lead to security vulnerabilities.

整数运算

无符号加法

我们先把整数加法细分一下：

无符号整数加法
有符号整数加法

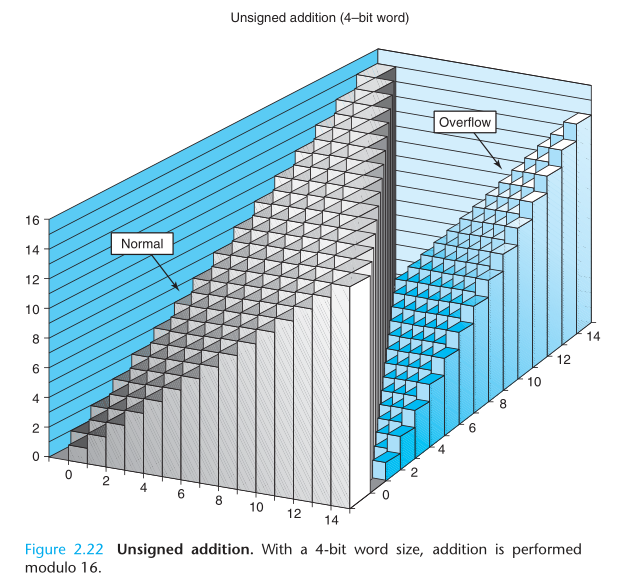
首先，两个 32 位无符号整数的和可能大于 32 位二进制能表示的最大值 UMax₃₂ = 2³² - 1，这时需要 33 位才能表示。如果只能用 32 位表示，那么只能把 33 位截断为 32 位。见公式 2.11。

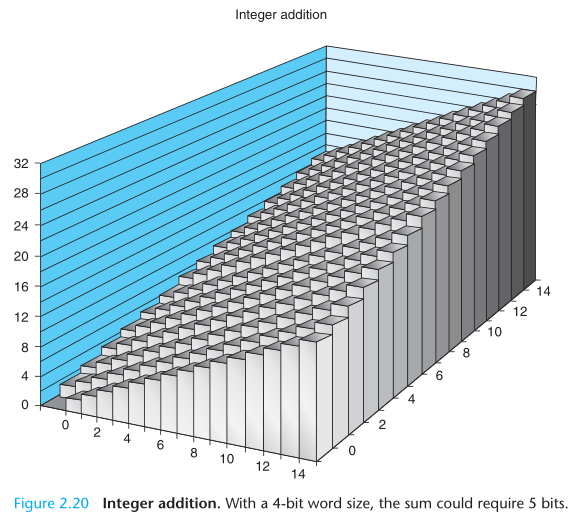
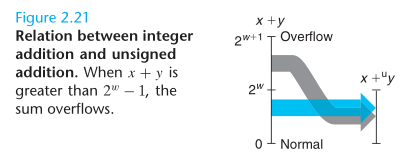
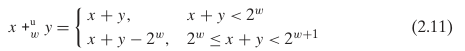
An arithmetic operation is said to overflow when the full integer result cannot fit within the word size limits of the data type.

对于阿贝尔群里的每个元素 x，总有一个加法逆元 x’，使得 x + x’ = 0。这里我的理解是，假设把 x 从十进制转换为二进制，假设 x 为 32 位，那么 x’ 就是 0x0 - x，见公式 2.12。

补码加法

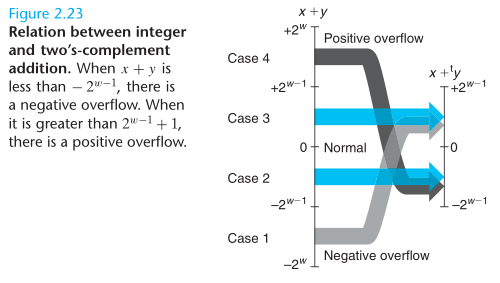
对于有符号整数（补码）加法，能细分出三种情况：

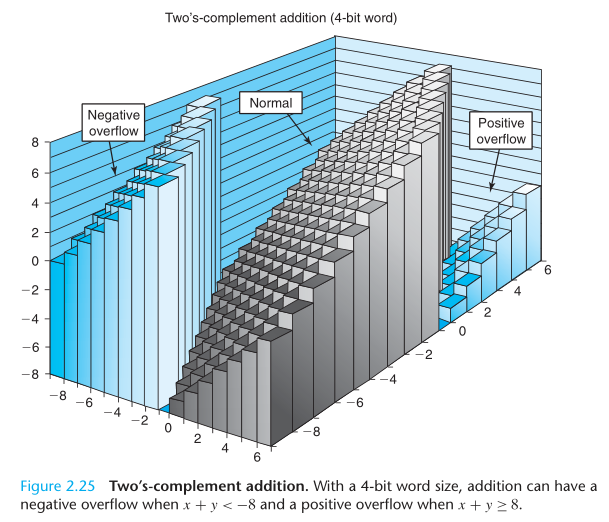
a + b > TMax，即和正溢出，最终的和为 a + b - 2³²
TMin <= a + b <= TMax，即和仍在取值范围
a + b < TMin，即和负溢出，最终的和为 a + b + 2³²

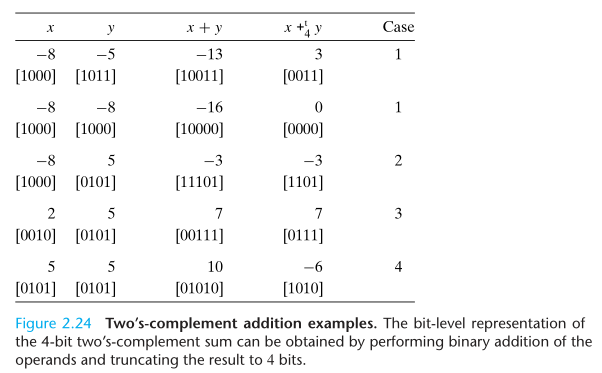
The w-bit two’s-complement sum of two numbers has the exact same bit-level representation as the unsigned sum. In fact, most computers use the same machine instruction to perform either unsigned or signed addition.

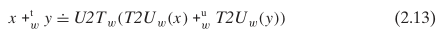
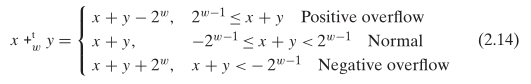
补码取反

接下来是整数取反，对于无符号整数，自然不存在取反操作。那么对于有符号整数 t，取反的值，也就是加法逆元，自然是 -t。但 TMin 比较特殊，其加法逆元是 TMin 自身。为了方便阐述，这里取 4 位有符号整数的 TMin = [1000]。要计算 TMin 的加法逆元 TMin’，显然 TMin’ 的低三位均是 0，最高位为 1，这样 TMin + TMin’ = [1000] + [1000] = [10000]，然后把最高位截掉，剩下 [0000]，可见 TMin’ = TMin。另一方面，因为 TMin + TMin = -2³ - 2³ = -2⁴ 负溢出，我们根据上面的公式 2.14，对于负溢出的和要加上 2^w，这里 w = 4，所以 TMin + TMin = -2⁴ + 2⁴ = 0，满足了阿贝尔群的特性。再次得出 TMin 的加法逆元是自身。

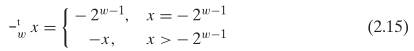
对于求一个 w 位有符号整数 x 二进制表示的加法逆元，方式很简单：

x = TMin，则加法逆元为 TMin。
x ≠ TMin，各位取反得到 x’，最后 x’ + 1。因为 x + x’ 会得到 w 位的 [11…1]，再加 1 就得到 w+1 位的 [100…0]，再把最高位截掉，就剩下 w 位的 [00…0]。

无符号乘法

对于 w 位的无符号整数的乘法 x * y = p，p 可能正溢出。因为 p 只保留 w 位，所以根据公式 2.9，只需要 p mod 2^w 即可。

补码乘法

有符号整数的乘法同理。

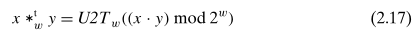
公式 2.8 证明了为什么 w 位无符号乘法和补码乘法得出的乘积，其二进制表示的低 w 位是一样的，其中 x, y 是补码，x’, y’ 是无符号：

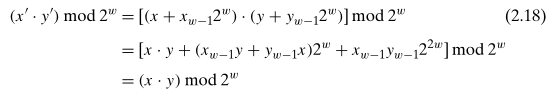
乘以常数

On most machines, the integer multiply instruction is fairly slow, requiring 10 or more clock cycles, whereas other integer operations - such as addition, subtraction, bit-level operations, and shifting - require only 1 clock cycle. As a consequence, one important optimization used by compilers is to attempt to replace multiplications by constant factors with combinations of shift and addition operations. We will first consider the case of multiplying by a power of 2, and then generalize this to arbitrary constants.

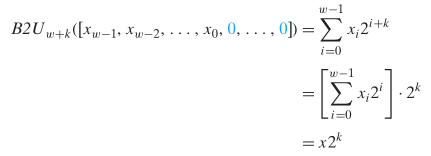
Given that integer multiplication is much more costly than shifting and adding, many C compilers try to remove many cases where an integer is being multiplied by a constant with combinations of shifting, adding, and subtracting. For example, suppose a program contains the expression x*14. Recognizing that 14 = 2³ + 2² + 2¹, the compiler can rewrite the multiplication as (x<<3) + (x<<2) + (x<<1), replacing one multiplication with three shifts and two additions.

除以 2 的幂

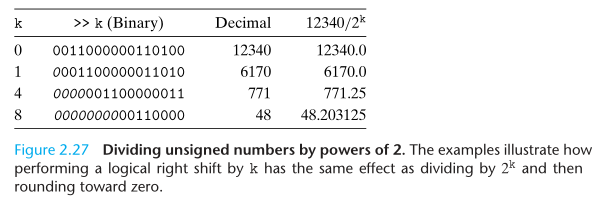
Integer division on most machines is even slower than integer multiplication - requiring 30 or more clock cycles. Dividing by a power of 2 can also be performed using shift operations, but we use a right shift rather than a left shift. The two different shifts - logical and arithmetic - serve this purpose for unsigned and two’s-complement numbers, respectively.

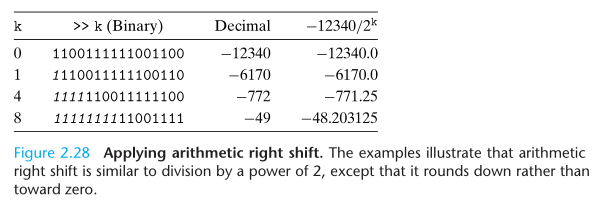
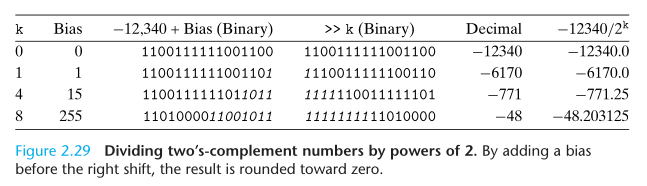
关于整数运算的最后思考

As we have seen, the “integer” arithmetic performed by computers is really a form of modular arithmetic.

We have especially seen that the unsigned data type, while conceptually straightforward, can lead to behaviors that even experienced programmers do not expect.

syawlaus

《深入理解计算机系统》学习笔记 - 第 2 章：信息的表示和处理