插入排序

发表于 2014-11-13   |   分类于 数据结构与算法

算法介绍

给定一个数字序列 1 6 8 4 2 5 3 9 7 0，想要排序为 0 1 2 3 4 5 6 7 8 9，有什么方法？（注：下面说的有序都默认为升序）

最简单的算法是：

  1. 仅包含第一个数的子序列是有序的
  2. 取出下一个数，如果它小于前一个数，就交换两个值的位置，一直比较，直到它大于等于前一个数，或到达了序列首
  3. 对于数字序列里每个数，重复步骤2

为什么这个算法被称为插入排序呢？因为：

  • 第一次排序后，仅包含第一个数的子序列是有序的
  • 第二次排序后，只包含前两个数的子序列是有序的
  • 第 N 次排序后，只包含前 N 个数的子序列是有序的
  • 第 N+1 次排序时，把第 N+1 个数插入到前 N 个数的有序子序列里的某个位置，使之成为包含前 N+1 个数的有序子序列

所以这个算法被称为插入排序。

可视化效果

这个链接给出插入排序的可视化效果（选择 InsertionSort）。

正确性证明

怎么证明这个算法是正确的？

因为涉及自然数的递推关系，所以容易联想用数学归纳法证明：

证明:

    * 当 n = 1 时，即当前排序的是序列里第一个数，插入排序算法成立，因为只有第一个数的子序列是有序的。
    * 假设当 n = k 时，即当前排序的是序列里第 k 个数，插入排序算法成立，即前 k 个数的子序列是有序的。

    需要证明：当 n = k+1 时，即当前排序的是序列里第 k+1 个数，插入排序算法成立，即前 k+1 个数的子序列是有序的。

    因为当 n = k 时，插入排序算法成立，前 k 个数已经有序，那么现在需要把第 k+1 个数排到前 k 个数的某个位置。
    因为第 k+1 个数与前面每一个数比较，如果小于前一个数，就交换位置，直到它大于等于前一个数，或到达了序列首。所以当第 k+1 个数停止交换位置时，它必然大于等于前一个数且小于后一个数，或到达序列首，即在前 k 个数的有序子序列的位置是中间/序列首/序列尾。这三种情况分别讨论。
        1. 在子序列中间：从题设知道，前 k 个数是有序的，而第 k+1 个数大于等于其当前位置的前一个数且小于后一个数，所以前 k+1 个数是有序的，这种情况证毕。
        2. 在子序列首：从题设知道，前 k 个数是有序的，而第 k+1 个数小于后一个数（即前 k 个数的第一个数），所以必然都小于前 k 个数，所以前 k+1 个数是有序的，这种情况证毕。
        3. 在子序列尾：从题设知道，前 k 个数是有序的，而第 k+1 个数大于等于前一个数（即前 k 个数的第 k 个数），所以必然都大于等于前 k 个数，所以前 k+1 个数是有序的，这种情况证毕。

    综上所述，证毕，上面的插入排序算法是正确的。

展开运行过程

在我们写伪代码前，把整个程序执行过程展开，以便我们写出代码：

index  0 1 2 3 4 5 6 7 8 9
value  1 6 8 4 2 5 3 9 7 0

第一次排序    1 6 8 4 2 5 3 9 7 0，outerIdx 为0，trackOuterIdx 为0，值为1
              done，即仅包含前1个数的子序列是有序的
第二次排序    1 6 8 4 2 5 3 9 7 0，outerIdx 为1，trackOuterIdx 为1，值为6，需要与 0 <= innerIdx <= 0 的值，即与 1 比较
              1 <= 6，done，即包含前2个数的子序列 1 6 是有序的
第三次排序    1 6 8 4 2 5 3 9 7 0，outerIdx 为2，trackOuterIdx 为2，值为8，需要与 0 <= innerIdx <= 1 的值，即与 1 6 比较
              6 <= 8，done，即包含前3个数的子序列 1 6 8 是有序的
第四次排序    1 6 8 4 2 5 3 9 7 0，outerIdx 为3，trackOuterIdx 为3，值为4，需要与 0 <= innerIdx <= 2 的值，即与 1 6 8 比较
              8 > 4，交换两个值，即 1 6 4 8，trackOuterIdx 减1后为2
              6 > 4，交换两个值，即 1 4 6 8，trackOuterIdx 减1后为1
              1 <= 4，done，即包含前4个数的子序列 1 4 6 8 是有序的
第五次排序    1 4 6 8 2 5 3 9 7 0，outerIdx 为4，trackOuterIdx 为4，值为2，需要与 0 <= innerIdx <= 3 的值，即与 1 4 6 8 比较
              8 > 2，交换两个值，即 1 4 6 2 8，trackOuterIdx 减1后为3
              6 > 2，交换两个值，即 1 4 2 6 8，trackOuterIdx 减1后为2
              4 > 2，交换两个值，即 1 2 4 6 8，trackOuterIdx 减1后为1
              1 <= 2，done，即包含前5个数的子序列 1 2 4 6 8 是有序的
第六次排序    1 2 4 6 8 5 3 9 7 0，outerIdx 为5，trackOuterIdx 为5，值为5，需要与 0 <= innerIdx <= 4 的值，即与 1 2 4 6 8 比较
              8 > 5，交换两个值，即 1 2 4 6 5 8，trackOuterIdx 减1后为4
              6 > 5，交换两个值，即 1 2 4 5 6 8，trackOuterIdx 减1后为3
              4 <= 5，done，即包含前6个数的子序列 1 2 4 5 6 8 是有序的
第七次排序    1 2 4 5 6 8 3 9 7 0，outerIdx 为6，trackOuterIdx 为6，值为3，需要与 0 <= innerIdx <= 5 的值，即与 1 2 4 5 6 8 比较
              8 > 3，交换两个值，即 1 2 4 5 6 3 8，trackOuterIdx 减1后为5
              6 > 3，交换两个值，即 1 2 4 5 3 6 8，trackOuterIdx 减1后为4
              5 > 3，交换两个值，即 1 2 4 3 5 6 8，trackOuterIdx 减1后为3
              4 > 3，交换两个值，即 1 2 3 4 5 6 8，trackOuterIdx 减1后为2
              2 <= 3，done，即包含前7个数的子序列 1 2 3 4 5 6 8 是有序的
第八次排序    1 2 3 4 5 6 8 9 7 0，outerIdx 为7，trackOuterIdx 为7，值为9，需要与 0 <= innerIdx <= 6 的值，即与 1 2 3 4 5 6 8 比较
              8 <= 9，done，即包含前8个数的子序列 1 2 3 4 5 6 8 9 是有序的
第九次排序    1 2 3 4 5 6 8 9 7 0，outerIdx 为8，trackOuterIdx 为8，值为7，需要与 0 <= innerIdx <= 7 的值，即与 1 2 3 4 5 6 8 9 比较
              9 > 7, 交换两个值，即 1 2 3 4 5 6 8 7 9，trackOuterIdx 减1后为7
              8 > 7, 交换两个值，即 1 2 3 4 5 6 7 8 9，trackOuterIdx 减1后为6
              6 <= 7，done，即包含前9个数的子序列 1 2 3 4 5 6 7 8 9 是有序的
第十次排序    1 2 3 4 5 6 7 8 9 0，outerIdx 为9，trackOuterIdx 为9，值为0，需要与 0 <= innerIdx <= 8 的值，即与 1 2 3 4 5 6 7 8 9 比较
              9 > 0，交换两个值，即 1 2 3 4 5 6 7 8 0 9，trackOuterIdx 减1后为8
              8 > 0，交换两个值，即 1 2 3 4 5 6 7 0 8 9，trackOuterIdx 减1后为7
              7 > 0，交换两个值，即 1 2 3 4 5 6 0 7 8 9，trackOuterIdx 减1后为6
              6 > 0，交换两个值，即 1 2 3 4 5 0 6 7 8 9，trackOuterIdx 减1后为5
              5 > 0，交换两个值，即 1 2 3 4 0 5 6 7 8 9，trackOuterIdx 减1后为4
              4 > 0，交换两个值，即 1 2 3 0 4 5 6 7 8 9，trackOuterIdx 减1后为3
              3 > 0，交换两个值，即 1 2 0 3 4 5 6 7 8 9，trackOuterIdx 减1后为2
              2 > 0，交换两个值，即 1 0 2 3 4 5 6 7 8 9，trackOuterIdx 减1后为1
              1 > 0，交换两个值，即 0 1 2 3 4 5 6 7 8 9，trackOuterIdx 减1后为0
              0 已经到达序列首，done，即包含前10个数的子序列 0 1 2 3 4 5 6 7 8 9 是有序的
第十一次排序  0 1 2 3 4 5 6 7 8 9，outerIdx 为10 > maxOuterIdx 9，整个插入排序过程结束，最终排序后的序列是：0 1 2 3 4 5 6 7 8 9

从上面的展开过程可以看到，程序里用到几个值：outerIdx, innerIdx, trackOuterIdx, maxOuterIdx，其中：

  • maxOuterIdx 即 size(a) - 1
  • outerIdx 为 [1, maxOuterIdx] 之间的正整数，用于遍历 N 次排序
  • innerIdx 为 [outerIdx - 1, 0] 之间的正整数，用于第 i 次排序时第 i 个数与前面的数比较
  • trackOuterIdx 是临时保存 outerIdx 的值，用于跟踪 outerIdx 的值在 innerIdx 循环里变化的位置

伪代码

伪代码如下：

a[] = {1 6 8 4 2 5 3 9 7 0}
for outerIdx 范围 [1, size(a) - 1]
    trackOuterIdx = outerIdx
    for innerIdx 范围 [outerIdx - 1, 0]
        if (a[innerIdx] <= a[trackOuterIdx])
            break    // 本次 inner 循环结束
        else
            swap(a[innerIdx], a[trackOuterIdx])  // 交换 idx 对应的值
            trackOuterIdx--

代码

根据伪代码，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <stdio.h>
void swap(int *pa, int *pb);
void printArray(int a[], int size);
int main() {
    int a[] = {1, 6, 8, 4, 2, 5, 3, 9, 7, 0};
    int outerIdx, innerIdx, trackOuterIdx, arraySize;
    // 排序前
    arraySize = sizeof(a) / sizeof(a[0]);
    printf("第1次排序后：");
    printArray(a, arraySize);
    // 排序中
    for (outerIdx = 1; outerIdx < arraySize; outerIdx++) {
        trackOuterIdx = outerIdx;
        for (innerIdx = outerIdx - 1; innerIdx >= 0; innerIdx--) {
            if (a[innerIdx] <= a[trackOuterIdx]) {
                break;
            }
            else {
                swap(&a[innerIdx], &a[trackOuterIdx]);
                trackOuterIdx--;
            }
        }
        printf("第%d次排序后: ", outerIdx + 1);
        printArray(a, arraySize);
    }
    
    // 排序后
    printf("\n最终排序后的序列: ");
    printArray(a, arraySize); 
    return 0;
}
void swap(int *pa, int *pb) {
    int temp;
    temp = *pa;
    *pa = *pb;
    *pb = temp;
}
void printArray(int a[], int arraySize) {
    int i;
    for (i = 0; i < arraySize; i++) {
        printf("%d ", a[i]);
    }
    printf("\n");
}

运行结果

第1次排序后：1 6 8 4 2 5 3 9 7 0 
第2次排序后: 1 6 8 4 2 5 3 9 7 0 
第3次排序后: 1 6 8 4 2 5 3 9 7 0 
第4次排序后: 1 4 6 8 2 5 3 9 7 0 
第5次排序后: 1 2 4 6 8 5 3 9 7 0 
第6次排序后: 1 2 4 5 6 8 3 9 7 0 
第7次排序后: 1 2 3 4 5 6 8 9 7 0 
第8次排序后: 1 2 3 4 5 6 8 9 7 0 
第9次排序后: 1 2 3 4 5 6 7 8 9 0 
第10次排序后: 0 1 2 3 4 5 6 7 8 9 

最终排序后的序列: 0 1 2 3 4 5 6 7 8 9

测试

怎么测试这个程序？(TODO)

时间复杂度

时间复杂度分析：

  • main() 第 1~2 行是变量的声明/定义工作，时间复杂度为 O(1)
  • 排序前 的代码是打印数组的函数，函数里有 for 循环，循环次数最多为 size(a)，时间复杂度为 O(n)
  • 排序中 有 for 循环，循环次数最多为 size(a)，时间复杂度为 O(n)
    • 嵌套 for 循环，循环次数最多为 size(a)-1，时间复杂度为 O(n)
    • 打印数组的函数，函数里有 for 循环（且嵌套在外层 for 循环里），循环次数最多为 size(arr)，时间复杂度为 O(n)
  • 第33~34行是打印数组的函数，函数里有 for 循环，循环次数最多为 size(arr)，时间复杂度为 O(n)

综上，程序的时间复杂度 = O(1) + O(n) + O(n*2n) + O(n) = O(n2)

空间复杂度

空间复杂度分析：

  • 第8行用到4个变量，空间复杂度为 O(1)
  • 第14、29、34行打印数组，用到1个变量，空间复杂度为 O(1)
  • 第23行交换两个内存地址的值，用到1个变量，空间复杂度为 O(1)

综上，程序的空间复杂度为 O(1)。

改进

上面的算法有一个很简单的改进方法：在步骤2，如果当前检查元素小于前一个元素时，无需交换两个元素的值，只需要把前一个元素后移，再继续检查，直到当前检查元素大于等于前一个元素，或到达序列首，就知道当前检查元素应该插入到有序子序列的位置。

可视化效果如下：

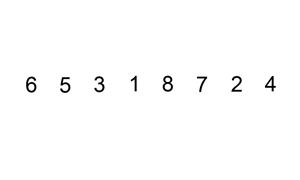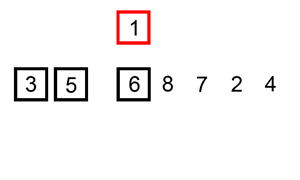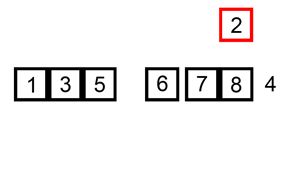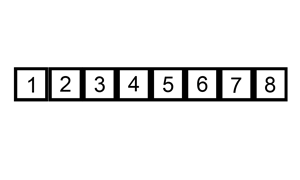
改进后的展开过程

对序列 1 6 8 4 2 5 3 9 7 0 排序的改进后的展开过程如下：

index  0 1 2 3 4 5 6 7 8 9
value  1 6 8 4 2 5 3 9 7 0

第一次排序    1 6 8 4 2 5 3 9 7 0，outerIdx 为0，值为1
              done，即仅包含前1个数的子序列是有序的
第二次排序    1 6 8 4 2 5 3 9 7 0，outerIdx 为1，值为6，需要与 0 <= innerIdx <= 0 的值，即与 1 比较
              1 <= 6，把6放在1后面，done，即包含前2个数的子序列 1 6 是有序的
第三次排序    1 6 8 4 2 5 3 9 7 0，outerIdx 为2，值为8，需要与 0 <= innerIdx <= 1 的值，即与 1 6 比较
              6 <= 8，把8放在6后面，done，即包含前3个数的子序列 1 6 8 是有序的
第四次排序    1 6 8 4 2 5 3 9 7 0，outerIdx 为3，值为4，需要与 0 <= innerIdx <= 2 的值，即与 1 6 8 比较
              8 > 4，把8后移一位，即 1 6 8 8
              6 > 4，把6后移一位，即 1 6 6 8
              1 <= 4，把4放在1后面，即 1 4 6 8，done，即包含前4个数的子序列 1 4 6 8 是有序的
第五次排序    1 4 6 8 2 5 3 9 7 0，outerIdx 为4，值为2，需要与 0 <= innerIdx <= 3 的值，即与 1 4 6 8 比较
              8 > 2，把8后移一位，即 1 4 6 8 8
              6 > 2，把6后移一位，即 1 4 6 6 8
              4 > 2，把4后移一位，即 1 4 4 6 8
              1 <= 2，把2放在1后面，即 1 2 4 6 8，done，即包含前5个数的子序列 1 2 4 6 8 是有序的
第六次排序    1 2 4 6 8 5 3 9 7 0，outerIdx 为5，值为5，需要与 0 <= innerIdx <= 4 的值，即与 1 2 4 6 8 比较
              8 > 5，把8后移一位，即 1 2 4 6 8 8
              6 > 5，把6后移一位，即 1 2 4 6 6 8
              4 <= 5，把5放在4后面，即 1 2 4 5 6 8，done，即包含前6个数的子序列 1 2 4 5 6 8 是有序的
第七次排序    1 2 4 5 6 8 3 9 7 0，outerIdx 为6，值为3，需要与 0 <= innerIdx <= 5 的值，即与 1 2 4 5 6 8 比较
              8 > 3，把8后移一位，即 1 2 4 5 6 8 8
              6 > 3，把6后移一位，即 1 2 4 5 6 6 8
              5 > 3，把5后移一位，即 1 2 4 5 5 6 8
              4 > 3，把4后移一位，即 1 2 4 4 5 6 8
              2 <= 3，把3放在2后面，即 1 2 3 4 5 6 8，done，即包含前7个数的子序列 1 2 3 4 5 6 8 是有序的
第八次排序    1 2 3 4 5 6 8 9 7 0，outerIdx 为7，值为9，需要与 0 <= innerIdx <= 6 的值，即与 1 2 3 4 5 6 8 比较
              8 <= 9，把9放在8后面，即 1 2 3 4 5 6 8 9，done，即包含前8个数的子序列 1 2 3 4 5 6 8 9 是有序的
第九次排序    1 2 3 4 5 6 8 9 7 0，outerIdx 为8，值为7，需要与 0 <= innerIdx <= 7 的值，即与 1 2 3 4 5 6 8 9 比较
              9 > 7，把9后移一位，即 1 2 3 4 5 6 8 9 9
              8 > 7，把8后移一位，即 1 2 3 4 5 6 8 8 9
              6 <= 7，把7放在6后面，即 1 2 3 4 5 6 7 8 9，done，即包含前9个数的子序列 1 2 3 4 5 6 7 8 9 是有序的
第十次排序    1 2 3 4 5 6 8 9 7 0，outerIdx 为9，值为0，需要与 0 <= innerIdx <= 8 的值，即与 1 2 3 4 5 6 7 8 9 比较
              9 > 0，把9后移一位，即 1 2 3 4 5 6 7 8 9 9
              8 > 0，把8后移一位，即 1 2 3 4 5 6 7 8 8 9
              7 > 0，把7后移一位，即 1 2 3 4 5 6 7 7 8 9
              6 > 0，把6后移一位，即 1 2 3 4 5 6 6 7 8 9
              5 > 0，把5后移一位，即 1 2 3 4 5 5 6 7 8 9
              4 > 0，把4后移一位，即 1 2 3 4 4 5 6 7 8 9
              3 > 0，把3后移一位，即 1 2 3 3 4 5 6 7 8 9
              2 > 0，把2后移一位，即 1 2 2 3 4 5 6 7 8 9
              1 > 0，把1后移一位，即 1 1 2 3 4 5 6 7 8 9
              0 到前序列首，把0放在首位，即 0 1 2 3 4 5 6 7 8 9，done，即包含前10个数的子序列 0 1 2 3 4 5 6 7 8 9 是有序的
第十一次排序  0 1 2 3 4 5 6 7 8 9，outerIdx 为10 > maxOuterIdx 9，整个插入排序过程结束，最终排序后的序列是：0 1 2 3 4 5 6 7 8 9

改进后的伪代码

我们看到，上面的展开过程用到：

  • maxOuterIdx，值为 size(a) - 1，即序列 a 的最大索引值
  • outerIdx，值为 [1, maxOuterIdx]，即从1到 maxOuterIdx 遍历，对每个数插入到前面已有序序列的某个位置
  • innerIdx，值为 [0, outerIdx - 1]，表示在本次 outerIdx 遍历过程中，遍历 outerIdx 前面的每个数，寻找出 outerIdx 的值需要插入的位置

伪代码如下：

for outerIdx from 1 to maxOuterIdx
    // 寻找出 outerIdx 的值需要插入的位置，前面的值 > 当前值，就后移一位，直到找到 <= 当前值的，就放在那个 idx 后面
    temp = a[outerIdx]
    foundInMiddle = false
    for innerIdx from outerIdx - 1 to 0
        if a[innerIdx] > temp
            a[innerIdx + 1] = a[innerIdx]   // 后移一位
        else
            a[innerIdx + 1] = a[outerIdx]   // 找到了插入位置
            foundInMiddle = true
            break
    if foundInMiddle == false
        a[0] = temp

改进后的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <stdio.h>
#define TRUE  1
#define FALSE 0
void printArray(int a[], int size);
int main() {
    int a[] = {1, 6, 8, 4, 2, 5, 3, 9, 7, 0};
    int size = sizeof(a) / sizeof(a[0]);
    int maxOutIdx = size - 1;
    int outerIdx;
    for (outerIdx = 1; outerIdx <= maxOutIdx; outerIdx++) {
        int temp = a[outerIdx];
        int foundInMiddle = FALSE;
        int innerIdx;
        for (innerIdx = outerIdx - 1; innerIdx >= 0; innerIdx--) {
            if (a[innerIdx] > temp) {
                a[innerIdx + 1] = a[innerIdx];  // 未找到插入位置，后移一位
            }
            else {
                a[innerIdx + 1] = temp;         // 找到了插入位置
                foundInMiddle = TRUE;
                break;
            }
        }
        if (! foundInMiddle) {
            a[0] = temp;
        }
    }
    // 排序完毕，打印结果
    printArray(a, size);
}
/**
 * 打印数组元素值
 * @param  数组, 数组大小
 * @return void
 */
void printArray(int a[], int size) {
    int i;
    for (i = 0; i < size; i++) {
        printf("%d ", a[i]);
    }
    printf("\n");
}

上面算法的时间复杂度还是 O(n2)，不太理想，还有其它更快的排序算法吗？

参考资料

版本控制简介