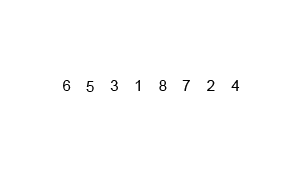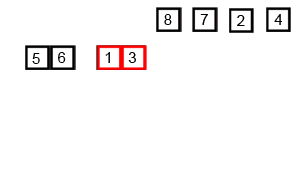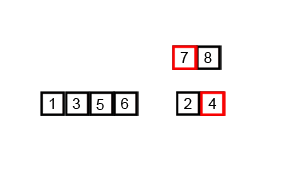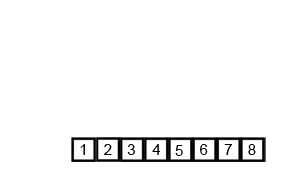合并排序

发表于 2016-05-04   |   分类于 数据结构与算法

算法介绍

还是数字序列的排序问题，给定一个数字序列 1 6 8 4 2 5 3 9 7 0，想要排序为 0 1 2 3 4 5 6 7 8 9，有什么方法？

与插入排序类似，能不能用分治来解决？

使用分治解决问题，需要把原问题分解为形式相同的子问题，解决子问题后，再把它们的结果合并为原问题的结果。对于排序问题，容易想到，子问题就是对子序列排序。那么问题转化为：怎么把原序列分解为子序列，在对子序列都排序后，把子序列组成为原序列的排序后结果。

可以考虑把原序列分解为两个子序列，元素数量为原序列的一半。对子序列排序后，再合并即是对原序列排序。

其中“对子序列排序”的过程，就是递归的过程。假设现在有数字序列 a，分解为两个子序列后，得到 a1、a2。对 a1 采用相同的方式，分解为 a11、a12。我们知道递归需要有 base case 才能结束，那么分解子序列过程的 base case 就是当子序列只有一个元素，只有一个元素的子序列自然是有序的。

这种思路的排序称为合并排序或归并排序（Merge sort）。

把 a 分解为 a1、a2 后，怎么合并 a1、a2 使得合并的结果也是有序的呢？设 a = [1, 6, 8, 4, 2, 5, 3, 9, 7, 0]，那么 a1 = [1, 6, 8, 4, 2]，a2 = [5, 3, 9, 7, 0]。排序后的 a1’ = [1, 2, 4, 6, 8]，a2’ = [0, 3, 5, 7, 9]，那么合并的思路就清晰了：

a1' = [1, 2, 4, 6, 8]
       ↑
       i1

a2' = [0, 3, 5, 7, 9]
       ↑
       i2

a' = []

比较 a1’[i1] 和 a2’[i2] 的值，因为 a2’[i2] 较小，所以 a’[0] = a2’[i2] = 0，i2 后移一位：

a1' = [1, 2, 4, 6, 8]
       ↑
       i1

a2' = [0, 3, 5, 7, 9]
          ↑
          i2

a' = [0]

比较 a1’[i1] 和 a2’[i2] 的值，因为 a1’[i1] 较小，所以 a[1] = a1’[i1] = 1，i1 后移一位：

a1' = [1, 2, 4, 6, 8]
          ↑
          i1

a2' = [0, 3, 5, 7, 9]
          ↑
          i2

a' = [0, 1]

一直重复这个过程，直到遍历完 a1’ 或 a2’ 的全部元素。在这个序列里，a1’ 会先遍历完，此时 a2’ 未遍历的元素只剩下 9：

a1' = [1, 2, 4, 6, 8]
                      ↑
                      i1 (完成遍历）

a2' = [0, 3, 5, 7, 9]
                   ↑
                   i2

a' = [0, 1, 2, 3, 4, 5, 6, 7, 8]

a2’ 剩下的全部元素，肯定比 a’ 中全部元素都大，且本身也有序，所以只要按顺序尾插入到 a’ 即可：

a' = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

接下来编写伪代码。因为需要遍历 a1’ 和 a2’，直到其中一个子序列遍历完毕，所以需要一个 while 循环，while 循环之后，再把未遍历完毕的子序列的剩下元素全部尾插入到 a’：

merge(a1, a2)
    size1 = size(a1')
    size2 = size(a2')
    i1 = i2 = 0
    while (i1 < size1 and i2 < size2)
        mergeSingleElement
    addToA

接下来我们编写 mergeSingleElement 和 addToA 的伪代码，先是 mergeSingleElement。

mergeSingleElement 要做的工作是：

  • 取 a1’[i1] 和 a2’[i2] 的较小值，尾插入到 a’
  • 相应的 index 后移一位

伪代码如下：

mergeSingleElement
    if (a1'[i1] < a2'[i2])
        a'[i] = a1'[i1]
        i1++
    else
        a'[i] = a2'[i1]
        i2++
    i++

addToA 要做的工作是：

  • 检查哪个子序列未完成遍历
  • 把未完成遍历的子序列剩下的元素，尾插入到 a’

伪代码如下：

addToA
    // a1' 未完成遍历
    if (i1 < size1)
        for i1 from i1 to (size1 - 1)
            add a1'[i1] to a'
    // a2' 未完成遍历
    if (i2 < size2)
        for i2 from i2 to (size2 - 1)
            add a2'[i2] to a'

分析完合并过程，我们回到分解子序列的过程：把序列 a 分解为两个子序列 a1 和 a2，对其进行排序后，再合并为 a’。对 a1 排序时，先把 a1 分解为 a11 和 a12，对其进行排序后，再合并为 a1’。一直分解，直到子序列只有一个元素（base case），自然就是有序的。分解过程的伪代码是：

mergeSort(a, minIndex, maxIndex)
    midIndex = (minIndex + maxIndex) / 2
    a1 = mergeSort(a, minIndex, midIndex)
    a2 = mergeSort(a, midIndex + 1, maxIndex)

可以看到，mergeSort 的过程是递归的，每一次递归，都把 a 的 [minIndex, maxIndex] 之间的元素组成的子序列分解为两个子序列的排序过程。在每一次递归前，都应先检查一下是否到达了 base case（minIndex >= maxIndex）。伪代码如下：

mergeSort(a, minIndex, maxIndex)
    if (minIndex >= maxIndex)   // base case
        return
    midIndex = (minIndex + maxIndex) / 2
    a1 = mergeSort(a, minIndex, midIndex)
    a2 = mergeSort(a, midIndex + 1, maxIndex)

或

mergeSort(a, minIndex, maxIndex)
    if (minIndex < maxIndex)
        midIndex = (minIndex + maxIndex) / 2
        a1 = mergeSort(a, minIndex, midIndex)
        a2 = mergeSort(a, midIndex + 1, maxIndex)

在得到有序的子序列 a1、a2 后，再将其合并为有序的原序列：

mergeSort(a, minIndex, maxIndex)
    if (minIndex < maxIndex)
        midIndex = (minIndex + maxIndex) / 2
        a1 = mergeSort(a, minIndex, midIndex)
        a2 = mergeSort(a, midIndex + 1, maxIndex)
        merge(a1, a2)

整个程序的伪代码，稍后在下面的小节整理给出。

可视化效果

我们先看看合并排序的可视化效果，从图形效果上感受一下这个算法是如何排序的，具体运行是怎样的。

（图片来源）

正确性证明

对 a 排序，先对两个子序列 a1、a2 排序，当 a1、a2 有序后进行合并，合并后 a 就是有序的。那么对 a1、a2 排序时同理。所以整个排序过程是正确的。

展开运行过程

运行过程可见上面的可视化效果。

伪代码

整合上面的算法分析过程的伪代码如下：

mergeSort(a, minIndex, maxIndex)
    if (minIndex < maxIndex)
        midIndex = (minIndex + maxIndex) / 2
        a1 = mergeSort(a, minIndex, midIndex)
        a2 = mergeSort(a, midIndex + 1, maxIndex)
        merge(a1, a2)

merge(a1, a2)
    size1 = size(a1')
    size2 = size(a2')
    i1 = i2 = 0
    while (i1 < size1 and i2 < size2)
        mergeSingleElement
    addToA

mergeSingleElement
    if (a1'[i1] < a2'[i2])
        a'[i] = a1'[i1]
        i1++
    else
        a'[i] = a2'[i1]
        i2++
    i++

addToA
    // a1' 未完成遍历
    if (i1 < size1)
        for i1 from i1 to (size1 - 1)
            add a1'[i1] to a'
    // a2' 未完成遍历
    if (i2 < size2)
        for i2 from i2 to (size2 - 1)
            add a2'[i2] to a'

代码

基本代码

伪代码用于描述算法的基本逻辑，只要逻辑没有问题即可。用代码描述则严格许多，在用代码描述上面几个函数前，先给出 main 函数框架：

1
2
3
4
5
6
7
8
9
#include <vector>
#include <iostream>
using namespace std;
int main() {
    vector<int> seq = { 1, 6, 8, 4, 2, 5, 3, 9, 7, 0 };
    mergeSort(seq, 0, seq.size());
    return 0;
}

接下来分别是上面几个函数。

首先是 mergeSort。

  • mergeSort 任务
    • 对一个无序序列进行排序，输出一个新的有序序列
  • 输入参数
    • 序列 seq
    • 对 seq 在范围 [minIndex, maxIndex] 内的子序列排序的下标最小值 minIndex，最大值 maxIndex
  • 输出
    • 一个长度跟原序列相同的新序列
1
2
3
4
5
6
7
8
9
10
11
12
vector<int> mergeSort(vector<int> seq,
                      int minIndex,
                      int maxIndex) {
    if (minIndex < maxIndex) {      // keep dividing
        int midIndex = (minIndex + maxIndex) / 2;
        vector<int> s1 = mergeSort(seq, minIndex, midIndex);
        vector<int> s2 = mergeSort(seq, midIndex + 1, maxIndex);
        vector<int> sortedSeq = merge(s1, s2);
        return sortedSeq;
    }
    return seq;     // reach base case, return seq itself
}

接下来是 merge。

  • merge 任务
    • 给定两个有序序列，合并为一个新的有序序列
  • 输入参数
    • 两个有序序列 s1、s2
  • 输出
    • 合并后的新的有序序列
1
2
3
4
5
6
7
8
9
10
11
vector<int> merge(vector<int> s1,
                  vector<int> s2) {
    int i1 = 0;
    int i2 = 0;
    vector<int> seq;
    while (i1 < s1.size() && i2 < s2.size()) {
        mergeSingleElement();
    }
    addToA();
    return seq;
}

接下来是 mergeSingleElement。

  • mergeSingleElement 任务
    • 取 s1、s2 未遍历的元素的最小值进行比较（即 a1’[i1] 和 a2’[i2]），取两者之间的较小值尾插入到 seq
    • 相应的 index（i1, i2）后移一位
  • 输入参数
    • 两个有序序列 s1、s2
    • s1、s2 当前未遍历的元素的最小值的下标 i1、i2
    • 需要尾插入的（合并后的）有序序列 seq
  • 输出
    • 无
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void mergeSingleElement(vector<int> s1,
                        int index1,
                        vector<int> s2,
                        int index2,
                        vector<int> seq) {
    if (s1[index1] < s2[index2]) {
        seq.push_back(s1[index1]);
        index1++;
    }
    else {
        seq.push_back(s2[index2]);
        index2++;
    }
}

接下来是 addToA。

  • addToA 任务
    • 检查哪个子序列未完成遍历
    • 把未完成遍历的子序列剩下的元素，尾插入到 seq
  • 输入参数
    • 两个有序序列 s1、s2
    • s1、s2 当前未遍历的元素的最小值的下标 i1、i2
    • 需要尾插入的（合并后的）有序序列 seq
  • 输出
    • 无
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void addToA(vector<int> s1,
            int index1,
            vector<int> s2,
            int index2,
            vector<int> seq) {
    // s1 未完成遍历
    int size1 = s1.size();
    if (index1 < size1) {
        for (int i = index1; i < size1; i++) {
            seq.push_back(s1[i]);
        }
    }
    // s2 未完成遍历
    int size2 = s2.size();
    if (index2 < size2) {
        for (int j = index2; j < size2; j++) {
            seq.push_back(s2[j]);
        }
    }
}

注意事项

按值传参

需要注意 C++ 的函数按值传参（pass by value）的问题。我们看看 mergeSingleElement 的函数定义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void mergeSingleElement(vector<int> s1,
                        int index1,
                        vector<int> s2,
                        int index2,
                        vector<int> seq) {
    if (s1[index1] < s2[index2]) {
        seq.push_back(s1[index1]);
        index1++;
    }
    else {
        seq.push_back(s2[index2]);
        index2++;
    }
}

可以看到，在 mergeSingleElement 里，把 s1[index1] 尾插入到 seq 后，index1++，但在函数返回后，index1++ 和 seq.push_back(s1[index1]) 后的新值无法在函数外生效（index2 同理，不再赘述）。而在后面的 addToA 函数中，需要用到 index1++ 和 seq.push_back(s1[index1]) 后的新值，所以需要修改 mergeSingleElement 中 index 和 vector 的传参方式，改为按引用传参（pass by reference）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void mergeSingleElement(vector<int>& s1,        // 按引用传参
                        int& index1,            // 按引用传参
                        vector<int>& s2,        // 按引用传参
                        int& index2,            // 按引用传参
                        vector<int>& seq) {     // 按引用传参
    if (s1[index1] < s2[index2]) {
        seq.push_back(s1[index1]);
        index1++;
    }
    else {
        seq.push_back(s2[index2]);
        index2++;
    }
}

还有相同的问题的函数还有 addToA、merge、mergeSort，修改为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
void addToA(vector<int>& s1,        // 按引用传参
            int& index1,            // 按引用传参
            vector<int>& s2,        // 按引用传参
            int& index2,            // 按引用传参
            vector<int>& seq) {     // 按引用传参
    // s1 未完成遍历
    int size1 = s1.size();
    if (index1 < size1) {
        for (int i = index1; i < size1; i++) {
            seq.push_back(s1[i]);
        }
    }
    // s2 未完成遍历
    int size2 = s2.size();
    if (index2 < size2) {
        for (int j = index2; j < size2; j++) {
            seq.push_back(s2[j]);
        }
    }
}
vector<int> merge(vector<int>& s1,      // 按引用传参
                  vector<int>& s2) {    // 按引用传参
    int i1 = 0;
    int i2 = 0;
    vector<int> seq;
    while (i1 < s1.size() && i2 < s2.size()) {
        mergeSingleElement(s1, i1, s2, i2, seq);
    }
    addToA(s1, i1, s2, i2, seq);
    return seq;
}
vector<int> mergeSort(vector<int>& seq,     // 按引用传参
                      int minIndex,
                      int maxIndex) {
    if (minIndex < maxIndex) {      // keep dividing
        int midIndex = (minIndex + maxIndex) / 2;
        vector<int> s1 = mergeSort(seq, minIndex, midIndex);
        vector<int> s2 = mergeSort(seq, midIndex + 1, maxIndex);
        vector<int> sortedSeq = merge(s1, s2);
        return sortedSeq;
    }
    return seq;     // reach base case, return seq itself
}

完整可运行代码

整合上面的代码后，得出可运行代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
/********************************************************************r******
* includes
*/
#include <vector>
#include <iostream>
/**************************************************************************
* namespaces
*/
using namespace std;
/*************************************************************************
* function prototypes
*/
vector<int> MergeSort(vector<int>& seq);
vector<int> mergeSort(vector<int>& seq,
                      int minIndex,
                      int maxIndex);
vector<int> merge(vector<int>& s1,
                  vector<int>& s2);
void mergeSingleElement(vector<int>& s1,
                        int& index1,
                        vector<int>& s2,
                        int& index2,
                        vector<int>& seq);
void addToA(vector<int>& s1,
            int& index1,
            vector<int>& s2,
            int& index2,
            vector<int>& seq);
/**************************************************************************
* function definitions
*/
vector<int> MergeSort(vector<int>& seq) {
    vector<int> sortedSeq = mergeSort(seq, 0, seq.size() - 1);
    return sortedSeq;
}
vector<int> mergeSort(vector<int>& seq,
                      int minIndex,
                      int maxIndex) {
    if (minIndex < maxIndex) {      // keep dividing
        int midIndex = (minIndex + maxIndex) / 2;
        vector<int> s1 = mergeSort(seq, minIndex, midIndex);
        vector<int> s2 = mergeSort(seq, midIndex + 1, maxIndex);
        vector<int> sortedSeq = merge(s1, s2);
        return sortedSeq;
    }
    else {      // reach base case
        vector<int> oneElementSeq;
        oneElementSeq.push_back(seq[minIndex]);
        return oneElementSeq;
    }
}
vector<int> merge(vector<int>& s1,
                  vector<int>& s2) {
    int i1 = 0;
    int i2 = 0;
    vector<int> seq;
    while (i1 < s1.size() && i2 < s2.size()) {
        mergeSingleElement(s1, i1, s2, i2, seq);
    }
    addToA(s1, i1, s2, i2, seq);
    return seq;
}
void mergeSingleElement(vector<int>& s1,
                        int& index1,
                        vector<int>& s2,
                        int& index2,
                        vector<int>& seq) {
    if (s1[index1] < s2[index2]) {
        seq.push_back(s1[index1]);
        index1++;
    }
    else {
        seq.push_back(s2[index2]);
        index2++;
    }
}
void addToA(vector<int>& s1,
            int& index1,
            vector<int>& s2,
            int& index2,
            vector<int>& seq) {
    // s1 未完成遍历
    int size1 = s1.size();
    if (index1 < size1) {
        for (int i = index1; i < size1; i++) {
            seq.push_back(s1[i]);
        }
    }
    // s2 未完成遍历
    int size2 = s2.size();
    if (index2 < size2) {
        for (int j = index2; j < size2; j++) {
            seq.push_back(s2[j]);
        }
    }
}
void printVector(vector<int>& seq) {
    for (int element : seq) {
        cout << element << " ";
    }
}
/**************************************************************************
* main entry
*/
int main() {
    vector<int> seq = { 1, 6, 8, 4, 2, 5, 3, 9, 7, 0 };
    vector<int> sortedSeq = MergeSort(seq);
    printVector(sortedSeq);
    return 0;
}

运行结果

0 1 2 3 4 5 6 7 8 9

测试

vector<int> seq = { 0, 0, 0, 0, 0, 0 };
运行结果：0 0 0 0 0 0 

vector<int> seq = { 0, 0, 1, 2, 3, 4 };
运行结果：0 0 1 2 3 4 

vector<int> seq = { 4, 3, 2, 1, 0, 0 };
运行结果：0 0 1 2 3 4

改进

上面程序的问题是，mergeSort 的 else 分支，当把 seq 分解到只有一个元素时（minIndex >= maxIndex），还创建了一个新的 vector 来保存该元素。这里不应该需要额外的内存，应做成 in-place（即当本次 mergeSort 只有一个元素时，就可返回，不需要输出），只有在 merge 两个有序子序列时，才需要额外分配内存。代码修改如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
/********************************************************************r******
* includes
*/
#include <vector>
#include <iostream>
/**************************************************************************
* namespaces
*/
using namespace std;
/*************************************************************************
* function prototypes
*/
void MergeSort2(vector<int>& seq);
void mergeSort2(vector<int>& seq,
                int minIndex,
                int maxIndex);
vector<int> merge2(vector<int>& seq,
                   int minIndex,
                   int midIndex,
                   int maxIndex);
void mergeSingleElement2(vector<int>& originSeq,
                         int& index1,
                         int& index2,
                         vector<int>& mergedSeq);
void addToA2(vector<int>& originSeq,
             int index1,
             int midIndex,
             int index2,
             int maxIndex,
             vector<int>& mergedSeq);
void replaceVector(vector<int>& originSeq,
                   int minIndex,
                   vector<int>& sortedSeq);
void printVector(vector<int>& seq);
/**************************************************************************
* function definitions
*/
void MergeSort2(vector<int>& seq) {
    mergeSort2(seq, 0, seq.size() - 1);
}
void mergeSort2(vector<int>& seq,
                int minIndex,
                int maxIndex) {
    // reach base case
    if (minIndex >= maxIndex) {
        return;     
    }
    // keep dividing
    int midIndex = (minIndex + maxIndex) / 2;
    mergeSort2(seq, minIndex, midIndex);        // mergeSort2 is in-place
    mergeSort2(seq, midIndex + 1, maxIndex);
    vector<int> sortedSeq = merge2(seq, minIndex, midIndex, maxIndex);      // merge2 is NOT in-place
    replaceVector(seq, minIndex, sortedSeq);
}
vector<int> merge2(vector<int>& seq,
                   int minIndex,
                   int midIndex,
                   int maxIndex) {
    int i1 = minIndex;
    int i2 = midIndex + 1;
    vector<int> mergedSeq;
    while (i1 <= midIndex && i2 <= maxIndex) {
        mergeSingleElement2(seq, i1, i2, mergedSeq);
    }
    addToA2(seq, i1, midIndex, i2, maxIndex, mergedSeq);
    return mergedSeq;
}
void mergeSingleElement2(vector<int>& originSeq,
                         int& index1,
                         int& index2,
                         vector<int>& mergedSeq) {
    if (originSeq[index1] < originSeq[index2]) {
        mergedSeq.push_back(originSeq[index1]);
        index1++;
    }
    else {
        mergedSeq.push_back(originSeq[index2]);
        index2++;
    }
}
void addToA2(vector<int>& originSeq,
             int index1,
             int midIndex,
             int index2,
             int maxIndex,
             vector<int>& mergedSeq) {
    // [minIndex, midIndex] 未完成遍历
    if (index1 <= midIndex) {
        for (int i = index1; i <= midIndex; i++) {
            mergedSeq.push_back(originSeq[i]);
        }
    }
    // [midIndex + 1, maxIndex] 未完成遍历
    if (index2 <= maxIndex) {
        for (int j = index2; j <= maxIndex; j++) {
            mergedSeq.push_back(originSeq[j]);
        }
    }
}
void replaceVector(vector<int>& originSeq,
                   int minIndex,
                   vector<int>& sortedSeq) {
    int i = minIndex;
    for (int n : sortedSeq) {
        originSeq[i] = n;
        i++;
    }
}
void printVector(vector<int>& seq) {
    for (int element : seq) {
        cout << element << " ";
    }
    cout << endl;
}
/**************************************************************************
* main entry
*/
int main() {
    vector<int> seq = { 1, 6, 8, 4, 2, 5, 3, 9, 7, 0 };
    MergeSort2(seq);
    printVector(seq);
    vector<int> seq2 = { 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 };
    MergeSort2(seq2);
    printVector(seq2);
    vector<int> seq3 = { 0, 0, 0, 4, 2, 5, 3, 9, 7, 0 };
    MergeSort2(seq3);
    printVector(seq3);
    return 0;
}
// 输出结果：
0 1 2 3 4 5 6 7 8 9 
0 1 2 3 4 5 6 7 8 9 
0 0 0 0 2 3 4 5 7 9

时间复杂度

如何分析递归程序的时间复杂度？

空间复杂度

如何分析递归程序的空间复杂度？

参考资料

DirectX 11 编程：常用 Windows API
C++ 函数：传参方式