Leetcode 题解 - 101. Symmetric Tree

发表于 2016-10-15   |   分类于 Leetcode

题目

给定一棵二叉树，检查它是否左右镜像对称。

示例：

例如，二叉树 [1, 2, 2, 3, 4, 4, 3] 是对称的：

    1
   / \
  2   2
 / \ / \
3  4 4  3

而二叉树 [1, 2, 2, null, 3, null, 3] 不对称：

  1
 / \
2   2
 \   \
 3    3

后续：

尝试分别用递归和迭代两种方式解决。

难度：容易

编程语言：C++

分析

程序框架为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode *root) {
        
    }
};

思路可以借鉴 Leetcode 题解 - 107. Binary Tree Level Order Traversal II，先把二叉树转换为 vector<vector<TreeNode*>>，每个元素是一个 vector<TreeNode*>，里面是第 i 层的所有 TreeNode 指针。然后根据 vector 下标能比较方便地判断二叉树是否对称。

我们先算出 vector<vector<TreeNode*>>，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
vector<vector<TreeNode*>> levelTopDown(TreeNode *root) {
    // 初始化
    vector<vector<TreeNode*>> vv;
    if (root == NULL) {
        return vv;
    }
    vector<TreeNode*> queue;
    vector<int> qLevel;
    queue.push_back(root);
    qLevel.push_back(1);
    // 循环构造 queue 和 qLevel
    for (int i = 0; i < queue.size(); i++) {
        TreeNode *node = queue[i];
        if (node == NULL) {
            continue;
        }
        queue.push_back(node->left);
        qLevel.push_back(qLevel[i] + 1);
        queue.push_back(node->right);
        qLevel.push_back(qLevel[i] + 1);
    }
    // 基于 queue 和 qLevel 正向构造 vv
    qLevel.insert(qLevel.begin(), 0);       // 头插入 sentinel 元素，方便统一循环
    for (int i = 0; i < queue.size(); i++) {
        if (qLevel[i] < qLevel[i + 1]) {    // 有 sentinel 元素后这个判断就可以统一
            vector<TreeNode*> vNewLevel;
            vv.push_back(vNewLevel);
        }
        vv[vv.size() - 1].push_back(queue[i]);
    }
    // vv 最后一层肯定全部是 NULL，整层去掉
    vv.erase(vv.end() - 1);
    return vv;
}

在上面代码的第 21、24 行，把 node->left 和 node->right（不管是否为 NULL）都添加到 queue 中。这样会导致一个问题，示例的第一棵二叉树层数为 3，上面的代码运行后生成的 vector<vector<TreeNode*>> 为：

[
    [1],
    [2, 2],
    [3, 4, 4, 3],
    [null, null, null, null, null, null, null, null]
]

即是多出来的最底一层全为 NULL。所以在 return vv 前把 vv 最后一个 vector<TreeNode*> 去掉。

在根据 vv 判断二叉树是否对称前，我们先整理一下完全二叉树各节点的下标：

    0
   / \
  1   2
 / \ / \
3  4 5  6

第 i 层有 2^(i-1) 个节点：

  • 第 1 层有 1 个节点
  • 第 2 层有 2 个节点
  • 第 3 层有 4 个节点
  • 第 4 层有 8 个节点

所以第 i 层的最左节点下标，即是前 i-1 层所有节点个数之和 + 1 - 1（-1 是因为下标从 0 开始），即 2^0 + 2^1 + … + 2^(i-2) = 2^(i-1) - 1，详见等比数列求和公式。

那么第 i 层的最右节点下标，即是最左节点下标 + 第 i 层节点个数 - 1，即 2^(i-1) - 1 + 2^(i-1) - 1 = 2^i - 2。

我们用一个表格来整理清楚各个数据：

层数    该层节点个数    最左节点下标    最右节点下标
  1          1               0               0
  2          2               1               2
  3          4               3               6
  4          8               7              14
  ...
  i       2^(i-1)        2^(i-1) - 1      2^i - 2

接下来就可以利用这些数据来判断二叉树是否对称了，思路是：

  1. 对于每一层，使用 leftIndex 和 rightIndex 记录该层的 vector<TreeNode*> 最左和最右节点下标
    • 如果 leftIndex 和 rightIndex 节点都为 NULL，则它们相同，leftIndex++，rightIndex–
    • 如果 leftIndex 和 rightIndex 只有一个为 NULL，则它们不相同，则整棵二叉树不对称，return false
    • 如果 leftIndex 和 rightIndex 节点都不为 NULL，则判断 leftVal == rightVal，相同则 leftIndex++，rightIndex–，否则整棵二叉树不对称，return false
  2. 对于二叉树每一层，重复第 1 步。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
class Solution {
public:
    bool isSymmetric(TreeNode *root) {
        if (root == NULL) {
            return true;
        }
        vector<vector<TreeNode*>> vv = levelTopDown(root);
        bool isSym = checkSymmetric(vv);
        return isSym;
    }
private:
    vector<vector<TreeNode*>> levelTopDown(TreeNode *root) {
        // 初始化
        vector<vector<TreeNode*>> vv;
        if (root == NULL) {
            return vv;
        }
        vector<TreeNode*> queue;
        vector<int> qLevel;
        queue.push_back(root);
        qLevel.push_back(1);
        // 循环构造 queue 和 qLevel
        for (int i = 0; i < queue.size(); i++) {
            TreeNode *node = queue[i];
            if (node == NULL) {
                continue;
            }
            queue.push_back(node->left);
            qLevel.push_back(qLevel[i] + 1);
            queue.push_back(node->right);
            qLevel.push_back(qLevel[i] + 1);
        }
        // 基于 queue 和 qLevel 正向构造 vv
        qLevel.insert(qLevel.begin(), 0);       // 头插入 sentinel 元素，方便统一循环
        for (int i = 0; i < queue.size(); i++) {
            if (qLevel[i] < qLevel[i + 1]) {    // 有 sentinel 元素后这个判断就可以统一
                vector<TreeNode*> vNewLevel;
                vv.push_back(vNewLevel);
            }
            vv[vv.size() - 1].push_back(queue[i]);
        }
        // vv 最后一层肯定全部是 NULL，整层去掉
        vv.erase(vv.end() - 1);
        return vv;
    }
    bool checkSymmetric(vector<vector<TreeNode*>>& vv) {
        int level = vv.size();
        for (int i = 1; i <= level; i++) {
            // 每层的初始 leftIndex, rightIndex
            int leftIndex = 0;
            int rightIndex = pow(2, i - 1) - 1;
            while (leftIndex <= rightIndex) {
                // 取左右两个节点
                TreeNode *leftNode = vv[i - 1][leftIndex];
                TreeNode *rightNode = vv[i - 1][rightIndex];
                // 两个都为 NULL
                if (leftNode == NULL && rightNode == NULL) {
                    leftIndex++;
                    rightIndex--;
                    continue;
                }
                // 有一个为 NULL
                if (leftNode == NULL || rightNode == NULL) {
                    return false;
                }
                // 两个都不为 NULL
                if (leftNode != NULL && rightNode != NULL) {
                    if (leftNode->val == rightNode->val) {
                        leftIndex++;
                        rightIndex--;
                        continue;
                    }
                    else {
                        return false;
                    }
                }
            }
        }
        return true;
    }
};

提交到 Leetcode，Runtime Error! 导致错误的输入是 [9, 71, 71, null, 79, 79, null, -76, -43, -43, -76, null, -52, 21, null, null, 84, -52]，即下面的二叉树：

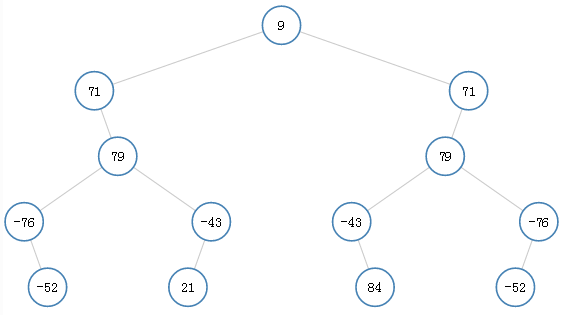
经 debug 后，我发现上面算法的问题出在 levelTopDown，因为 checkSymmetric 时最左节点下标都是从 0 开始，所以如果二叉树某一层的最左节点下标，不是完全二叉树意义上的最左节点（如第 3 层的第一个 79，第 5 层的第一个 -52），就会导致该层的下标不准确，导致访问 rightIndex 元素时 out of range，导致 Runtime Error。

简单来讲，即是 checkSymmetric 需要形参 vv 在第 i 层有 2^(i-1) 个元素，而 levelTopDown 返回的 vv 不满足。

如果把第 44~52 行的 for 循环修改为：

1
2
3
4
5
6
7
8
9
for (int i = 0; i < queue.size(); i++) {
    TreeNode *node = queue[i];
    queue.push_back(node == NULL ? NULL : node->left);
    qLevel.push_back(qLevel[i] + 1);
    queue.push_back(node == NULL ? NULL : node->right);
    qLevel.push_back(qLevel[i] + 1);
}

则满足第 i 层节点个数为 2^(i-1)，但会导致死循环。以上图二叉树为例，在第 5 层叶子节点下面层的节点全为 NULL，一层一层生成，无法停止。现在我还没想到办法如何判断出第 6 层全为 NULL 后则停止 for 循环，并把第 6 层删除。

想到办法了，在每次遍历 i 时，先判断是否 qLevel[i-1] < qLevel[i]，若是，则说是 queue[i] 是下一层的第一个节点。然后遍历上一层，如果全是 NULL，则 break 出 for 循环。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include <frequently-used-code-snippets.h>
#include <math.h>
using namespace std;
class Solution {
public:
    bool isSymmetric(TreeNode *root) {
        if (root == NULL) {
            return true;
        }
        vector<vector<TreeNode*>> vv = levelTopDown(root);
        bool isSym = checkSymmetric(vv);
        return isSym;
    }
private:
    vector<vector<TreeNode*>> levelTopDown(TreeNode *root) {
        // 初始化
        vector<vector<TreeNode*>> vv;
        if (root == NULL) {
            return vv;
        }
        vector<TreeNode*> queue;
        vector<int> qLevel;
        queue.push_back(root);
        qLevel.push_back(1);
        // 循环构造 queue 和 qLevel
        for (int i = 0; i < queue.size(); i++) {
            // 检查是否该停止 for 死循环
            if (i > 0 && qLevel[i - 1] < qLevel[i]) {   // i 是新的一层的最左节点下标
                bool continueFor = false;
                for (int j = i - 1; j >= 0 && qLevel[j] == qLevel[i - 1]; j--) {
                    if (queue[j] != NULL)   // 上一层有真实节点 {
                        continueFor = true;
                    }
                }
                if (! continueFor) {
                    break;
                }
            }
            // 继续循环
            TreeNode *node = queue[i];
            queue.push_back(node == NULL ? NULL : node->left);
            qLevel.push_back(qLevel[i] + 1);
            queue.push_back(node == NULL ? NULL : node->right);
            qLevel.push_back(qLevel[i] + 1);
        }
        // 基于 queue 和 qLevel 正向构造 vv
        qLevel.insert(qLevel.begin(), 0);       // 头插入 sentinel 元素，方便统一循环
        for (int i = 0; i < queue.size(); i++) {
            if (qLevel[i] < qLevel[i + 1]) {    // 有 sentinel 元素后这个判断就可以统一
                vector<TreeNode*> vNewLevel;
                vv.push_back(vNewLevel);
            }
            vv[vv.size() - 1].push_back(queue[i]);
        }
        // vv 最后两层肯定全部是 NULL，全部去掉
        vv.erase(vv.end() - 1);
        vv.erase(vv.end() - 1);
        return vv;
    }
    bool checkSymmetric(vector<vector<TreeNode*>>& vv) {
        int level = vv.size();
        for (int i = 1; i <= level; i++) {
            // 每层的初始 leftIndex, rightIndex
            int leftIndex = 0;
            int rightIndex = pow(2, i - 1) - 1;
            while (leftIndex <= rightIndex) {
                // 取左右两个节点
                TreeNode *leftNode = vv[i - 1][leftIndex];
                TreeNode *rightNode = vv[i - 1][rightIndex];
                // 两个都为 NULL
                if (leftNode == NULL && rightNode == NULL) {
                    leftIndex++;
                    rightIndex--;
                    continue;
                }
                // 有一个为 NULL
                if (leftNode == NULL || rightNode == NULL) {
                    return false;
                }
                // 两个都不为 NULL
                if (leftNode != NULL && rightNode != NULL) {
                    if (leftNode->val == rightNode->val) {
                        leftIndex++;
                        rightIndex--;
                        continue;
                    }
                    else {
                        return false;
                    }
                }
            }
        }
        return true;
    }
};

提交到 Leetcode，Time Limit Exceeded! 导致超时的输入为 [6, 82, 82, null, 53, 53, null, -58, null, null, -58, null, -85, -85, null, -9, null, null, -9, null, 48, 48, null, 33, null, null, 33, 81, null, null, 81, 5, null, null, 5, 61, null, null, 61, null, 9, 9, null, 91, null, null, 91, 72, 7, 7, 72, 89, null, 94, null, null, 94, null, 89, -27, null, -30, 36, 36, -30, null, -27, 50, 36, null, -80, 34, null, null, 34, -80, null, 36, 50, 18, null, null, 91, 77, null, null, 95, 95, null, null, 77, 91, null, null, 18, -19, 65, null, 94, null, -53, null, -29, -29, null, -53, null, 94, null, 65, -19, -62, -15, -35, null, null, -19, 43, null, -21, null, null, -21, null, 43, -19, null, null, -35, -15, -62, 86, null, null, -70, null, 19, null, 55, -79, null, null, -96, -96, null, null, -79, 55, null, 19, null, -70, null, null, 86, 49, null, 25, null, -19, null, null, 8, 30, null, 82, -47, -47, 82, null, 30, 8, null, null, -19, null, 25, null, 49]

上面代码的时间复杂度是 O(2^n)，因为最坏情况是二叉树每层只有一个节点，但为了保证 leftIndex 和 rightIndex 的正确性，要把该层所有 2^(i-1)-1 个节点全部都用 NULL 填充占位。所以当有 n 个节点，每个节点占一层时，n 层完全二叉树共有 2^0 + 2^1 + 2^2 + … + 2^(n-1) = 2^n - 1 个节点，所以时间复杂度为 O(2^n)。

#思路二

上面的思路好像走不通，那么就换个思路。要判断一棵二叉树是否对称，一个比较直观的思路是，对源二叉树生成一棵左右交换（即垂直旋转）的二叉树，如果两棵二叉树完全相同，那么源二叉树就是对称的。

代码如下：

1
2
3
4
5
bool isSymmetric(TreeNode *root) {
    TreeNode *invertRoot = invertTree(root);
    bool isSym = isSameTree(root, invertRoot);
    return isSym;
}

invertTree 可直接使用 Leetcode 题解 - 226. Invert Binary Tree 的代码。注意那是使用原地反转二叉树，在本题套用前，要先对二叉树作一份拷贝。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
TreeNode* invertTree(TreeNode *root) {
    TreeNode *copyRoot = copyTree(root);
    copyRoot = invertTreeInPlace(copyRoot);
    return copyRoot;
}
TreeNode* copyTree(TreeNode *root) {
    if (root == NULL) {
        return NULL;
    }
    TreeNode *copyRoot = new TreeNode(root->val);
    copyRoot->left = copyTree(root->left);
    copyRoot->right = copyTree(root->right);
    return copyRoot;
}
TreeNode* invertTreeInPlace(TreeNode *root) {
    // root 为空结点
    if (root == NULL) {
        return NULL;
    }
    // root 是叶子节点
    if (root->left == NULL &&
        root->right == NULL) {
        return root;
    }
    // 反转左子树
    TreeNode *left = invertTreeInPlace(root->left);
    // 反转右子树
    TreeNode *right = invertTreeInPlace(root->right);
    // 交换左右子结点
    TreeNode *temp = root->left;
    root->left = root->right;
    root->right = temp;
    // 返回根结点
    return root;
}

isSameTree 可直接使用 Leetcode 题解 - 100. Same Tree 的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
bool isSameTree(TreeNode *p, TreeNode *q) {
    
    if (p == NULL && q == NULL) {
        return true;
    }
    // 结构不同
    if (p != NULL && q == NULL) {
        return false;
    }
    // 结构不同
    if (p == NULL && q != NULL) {
        return false;
    }
    // 结构相同
    else {      // 即 p != NULL && q != NULL
        // 值不同
        if (p->val != q->val) {
            return false;
        }
        bool isSameLeft = isSameTree(p->left, q->left);
        bool isSameRight = isSameTree(p->right, q->right);
        if (isSameLeft && isSameRight) {
            return true;
        }
        return false;
    }
}

整个程序的代码如下（测试数据仍是下图的二叉树）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
#include <frequently-used-code-snippets.h>
#include <math.h>
using namespace std;
class Solution {
public:
    bool isSymmetric(TreeNode *root) {
        TreeNode *invertRoot = invertTree(root);
        bool isSym = isSameTree(root, invertRoot);
        return isSym;
    }
private:
    TreeNode* invertTree(TreeNode *root) {
        TreeNode *copyRoot = copyTree(root);
        copyRoot = invertTreeInPlace(copyRoot);
        return copyRoot;
    }
    TreeNode* copyTree(TreeNode *root) {
        if (root == NULL) {
            return NULL;
        }
        TreeNode *copyRoot = new TreeNode(root->val);
        copyRoot->left = copyTree(root->left);
        copyRoot->right = copyTree(root->right);
        return copyRoot;
    }
    TreeNode* invertTreeInPlace(TreeNode *root) {
        // root 为空结点
        if (root == NULL) {
            return NULL;
        }
        // root 是叶子节点
        if (root->left == NULL &&
            root->right == NULL) {
            return root;
        }
        // 反转左子树
        TreeNode *left = invertTreeInPlace(root->left);
        // 反转右子树
        TreeNode *right = invertTreeInPlace(root->right);
        // 交换左右子结点
        TreeNode *temp = root->left;
        root->left = root->right;
        root->right = temp;
        // 返回根结点
        return root;
    }
     bool isSameTree(TreeNode *p, TreeNode *q) {
        if (p == NULL && q == NULL) {
            return true;
        }
        // 结构不同
        if (p != NULL && q == NULL) {
            return false;
        }
        // 结构不同
        if (p == NULL && q != NULL) {
            return false;
        }
        // 结构相同
        else {      // 即 p != NULL && q != NULL
            // 值不同
            if (p->val != q->val) {
                return false;
            }
            // 值相同
            bool isSameLeft = isSameTree(p->left, q->left);
            bool isSameRight = isSameTree(p->right, q->right);
            if (isSameLeft && isSameRight) {
                return true;
            }
            return false;
        }
    }
};
int main() {
    // 设置二叉树
    TreeNode A(9);
    TreeNode B(71);
    TreeNode C(71);
    TreeNode D(79);
    TreeNode E(79);
    TreeNode F(-76);
    TreeNode G(-43);
    TreeNode H(-43);
    TreeNode I(-76);
    TreeNode J(-52);
    TreeNode K(21);
    TreeNode L(84);
    TreeNode M(-52);
    A.left = &B;
    A.right = &C;
    B.right = &D;
    C.left = &E;
    D.left = &F;
    D.right = &G;
    E.left = &H;
    E.right = &I;
    F.right = &J;
    G.left = &K;
    H.right = &L;
    I.left = &M;
    // Solution
    Solution sol;
    cout << sol.isSymmetric(&A) << endl;
}
// 输出结果：
// 0

提交到 Leetcode，Accepted! :) 运行时间为 9ms。

Leetcode 题解 - 107. Binary Tree Level Order Traversal II
Leetcode 题解 - 27. Remove Element