Leetcode 题解 - 104. Maximum Depth of Binary Tree

题目

给出一棵二叉树，求出其最大深度。

最大深度即是，从根结点到最远的叶子结点的最长路径上的结点数量。

难度：容易

编程语言：C++

---

分析

程序框架为：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {

    }
};

题目求二叉树最大深度，那我们先看看二叉树是怎样的，见下图：

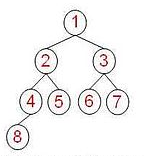
结点 1 为根结点，每往下一层，深度 + 1：

• 结点 1 深度为 1
• 结点 2～3 深度为 2
• 结点 4～7 深度为 3
• 结点 8 深度为 4

这棵二叉树的最大深度就是 1 -> 2 -> 4 -> 8 这条最长路径上的结点数量 4。

可以看出，二叉树是递归的结构，以 1 为根结点是二叉树，以其左右子结点为根结点的子树也是二叉树。所以要求 1 为根结点的二叉树的最大深度，只要先求出以 2 为根结点的左子树的最大深度，以及以 3 为根结点的右子树的最大深度，取两者较大值，再 + 1 即可。伪代码如下：

int maxDepth(TreeNode* root)
    if (root 为空结点)
        return 0

    if (root 为叶子结点)
        return 1

    int leftMaxDepth = maxDepth(root 左子结点）
    int rightMaxDepth = maxDepth(root 右子结点）
    return max(leftMaxDepth, rightMaxDepth) + 1

代码如下：

#include <iostream>
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;

    // constructor
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
public:
    int maxDepth(TreeNode* root) {
        // root 为空结点
        if (root == NULL) {
            return 0;
        }

        // root 为叶子节点
        if (root->left == NULL &&
            root->right == NULL) {
            return 1;
        }

        // 计算 root 左子树深度
        int leftMaxDepth = maxDepth(root->left);

        // 计算 root 右子树深度
        int rightMaxDepth = maxDepth(root->right);

        // 以当前节点为根节点的树的最大深度 = max(当前节点的左子树最大深度, 当前节点的右子树最大深度) + 1
        return (leftMaxDepth >= rightMaxDepth) ? (leftMaxDepth + 1) : (rightMaxDepth + 1);
    }
};

int main() {
    TreeNode node8(8);

    TreeNode node7(7);

    TreeNode node6(6);

    TreeNode node5(5);

    TreeNode node4(4);
    node4.left = &node8;

    TreeNode node3(3);
    node3.left = &node6;
    node3.right = &node7;

    TreeNode node2(2);
    node2.left = &node4;
    node2.right = &node5;

    TreeNode node1(1);
    node1.left = &node2;
    node1.right = &node3;

    Solution sol;
    int maxDepth = sol.maxDepth(&node1);
    cout << maxDepth << endl;
}

// 输出结果：
// 4

把 Solution 提交到 Leetcode，Accepted! :) 运行时间为 8ms。