Leetcode 题解 - 223. Rectangle Area

发表于 2016-11-02   |   分类于 Leetcode

题目

在一个 2D 平面上，有两个重叠的直线矩形，计算总面积。

每个矩形由左下角和右上角的顶点坐标定义，如下图：

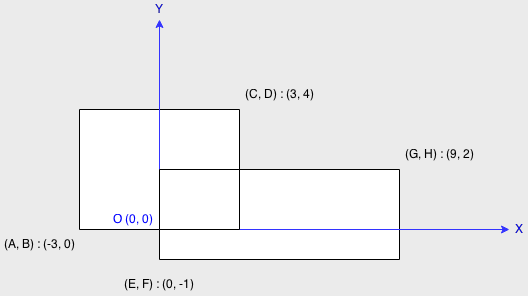
假设总面积不会超过 int 的最大值。

难度：容易

编程语言：C++

分析

程序框架为：

1
2
3
4
5
6
class Solution {
public:
    int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
        
    }
};

我们知道，总面积＝矩形 1 面积＋矩形 2 面积－重叠面积。所以先计算出示例图中重叠的矩形的面积，它的左下角顶点坐标为 (0, 0)，右上角顶点坐标为 (3, 2)，所以重叠面积是 (y2-y1) * (x2-x1) = 6。

我们把 ABCD 组成的矩形记为 □ABCD，把 EFGH 组成的矩形记为 □EFGH，把重叠矩形记为 □MNOP，并把重叠情况画成下面的图：

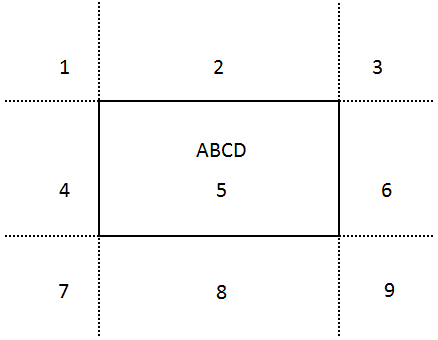
(E,F) 和 (G,H) 都有可能落在区域 1～9 里，所以我们分情况讨论：

  1. (E,F) 在区域 1，那么 (G,H) 在：
    1.1. 区域 1，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
    1.2. 区域 2，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
    1.3. 区域 3，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
  2. (E,F) 在区域 2，那么 (G,H) 在：
    2.2. 区域 2，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
    2.3. 区域 3，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
  3. (E,F) 在区域 3，那么 (G,H) 在：
    3.3. 区域 3，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
  4. (E,F) 在区域 4，那么 (G,H) 在：
    4.1. 区域 1，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
    4.2. 区域 2，形成的矩形跟 □ABCD 重叠，(M,N) = (A,F)，(O,P) = (G,D)
    4.3. 区域 3，形成的矩形跟 □ABCD 重叠，(M,N) = (A,F)，(O,P) = (C,D)
    4.4. 区域 4，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
    4.5. 区域 5，形成的矩形跟 □ABCD 重叠，(M,N) = (A,F)，(O,P) = (G,H)
    4.6. 区域 6，形成的矩形跟 □ABCD 重叠，(M,N) = (A,F)，(O,P) = (C,H)
  5. (E,F) 在区域 5，那么 (G,H) 在：
    5.1. 区域 2，形成的矩形跟 □ABCD 重叠，(M,N) = (E,F)，(O,P) = (G,D)
    5.2. 区域 3，形成的矩形跟 □ABCD 重叠，(M,N) = (E,F)，(O,P) = (C,D)
    5.3. 区域 5，形成的矩形跟 □ABCD 重叠，(M,N) = (E,F)，(O,P) = (G,H)
    5.4. 区域 6，形成的矩形跟 □ABCD 重叠，(M,N) = (E,F)，(O,P) = (C,H)
  6. (E,F) 在区域 6，那么 (G,H) 在：
    6.1. 区域 3，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
    6.2. 区域 6，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
  7. (E,F) 在区域 7，那么 (G,H) 在：
    7.1. 区域 1，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
    7.2. 区域 2，形成的矩形跟 □ABCD 重叠，(M,N) = (A,B)，(O,P) = (G,D)
    7.3. 区域 3，形成的矩形跟 □ABCD 重叠，(M,N) = (A,B)，(O,P) = (C,D)
    7.4. 区域 4，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
    7.5. 区域 5，形成的矩形跟 □ABCD 重叠，(M,N) = (A,B)，(O,P) = (G,H)
    7.6. 区域 6，形成的矩形跟 □ABCD 重叠，(M,N) = (A,B)，(O,P) = (C,H)
    7.7. 区域 7，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
    7.8. 区域 8，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
    7.9. 区域 9，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
  8. (E,F) 在区域 8，那么 (G,H) 在：
    8.1. 区域 2，形成的矩形跟 □ABCD 重叠，(M,N) = (E,B)，(O,P) = (G,D)
    8.2. 区域 3，形成的矩形跟 □ABCD 重叠，(M,N) = (E,B)，(O,P) = (C,D)
    8.3. 区域 5，形成的矩形跟 □ABCD 重叠，(M,N) = (E,B)，(O,P) = (G,H)
    8.4. 区域 6，形成的矩形跟 □ABCD 重叠，(M,N) = (E,B)，(O,P) = (C,H)
    8.5. 区域 8，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
    8.6. 区域 9，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
  9. (E,F) 在区域 9，那么 (G,H) 在：
    9.1. 区域 3，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
    9.2. 区域 6，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0
    9.3. 区域 9，形成的矩形跟 □ABCD 不重叠，所以重叠面积为 0

□MNOP 的面积 = (O-M) * (P-N)，然后总面积 = □ABCD + □EFGH - □MNOP，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
#include <frequently-used-code-snippets.h>
int COOR_A;
int COOR_B;
int COOR_C;
int COOR_D;
class Solution {
public:
    int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
        int area1 = (C - A) * (D - B);
        int area2 = (G - E) * (H - F);
        int overlapArea = computeOverlapArea(A, B, C, D, E, F, G, H);
        return area1 + area2 - overlapArea;
    }
private:
    int computeOverlapArea(int A, int B, int C, int D, int E, int F, int G, int H) {
        // 把 ABCD 保存到全局变量里
        COOR_A = A;
        COOR_B = B;
        COOR_C = C;
        COOR_D = D;
        
        int M = 0;
        int N = 0;
        int O = 0;
        int P = 0;
        // 4
        if (isInArea4(E, F)) {
            // 4.2
            if (isInArea2(G, H)) {
                M = A;
                N = F;
                O = G;
                P = D;
            }
            // 4.3
            else if (isInArea3(G, H)) {
                M = A;
                N = F;
                O = C;
                P = D;
            }
            // 4.5
            else if (isInArea5(G, H)) {
                M = A;
                N = F;
                O = G;
                P = H;
            }
            // 4.6
            else if (isInArea6(G, H)) {
                M = A;
                N = F;
                O = C;
                P = H;
            }
        }
        // 5
        else if (isInArea5(E, F)) {
            // 5.2
            if (isInArea2(G, H)) {
                M = E;
                N = F;
                O = G;
                P = D;
            }
            // 5.3
            else if (isInArea3(G, H)) {
                M = E;
                N = F;
                O = C;
                P = D;
            }
            // 5.5
            else if (isInArea5(G, H)) {
                M = E;
                N = F;
                O = G;
                P = H;
            }
            // 5.6
            else if (isInArea6(G, H)) {
                M = E;
                N = F;
                O = C;
                P = H;
            }
        }
        // 7
        else if (isInArea7(E, F)) {
            // 7.2
            if (isInArea2(G, H)) {
                M = A;
                N = B;
                O = G;
                P = D;
            }
            // 7.3
            else if (isInArea3(G, H)) {
                M = A;
                N = B;
                O = C;
                P = D;
            }
            // 7.5
            else if (isInArea5(G, H)) {
                M = A;
                N = B;
                O = G;
                P = H;
            }
            // 7.6
            else if (isInArea6(G, H)) {
                M = A;
                N = B;
                O = C;
                P = H;
            }
        }
        // 8
        else if (isInArea8(E, F)) {
            // 8.2
            if (isInArea2(G, H)) {
                M = E;
                N = B;
                O = G;
                P = D;
            }
            // 8.3
            else if (isInArea3(G, H)) {
                M = E;
                N = B;
                O = C;
                P = D;
            }
            // 8.5
            else if (isInArea5(G, H)) {
                M = E;
                N = B;
                O = G;
                P = H;
            }
            // 8.6
            else if (isInArea6(G, H)) {
                M = E;
                N = B;
                O = C;
                P = H;
            }
        }
        return (O - M) * (P - N);
    }
    bool isInArea2(int x, int y) {
        return (COOR_A <= x && x <= COOR_C && COOR_D <= y);
    }
    bool isInArea3(int x, int y) {
        return (COOR_C <= x && COOR_D <= y);
    }
    bool isInArea4(int x, int y) {
        return (x <= COOR_A && COOR_B <= y && y <= COOR_D);
    }
    bool isInArea5(int x, int y) {
        return (COOR_A <= x && x <= COOR_C && COOR_B <= y && y <= COOR_D);
    }
    bool isInArea6(int x, int y) {
        return (COOR_C <= x && COOR_B <= y && y <= COOR_D);
    }
    
    bool isInArea7(int x, int y) {
        return (x <= COOR_A && y <= COOR_B);
    }
    bool isInArea8(int x, int y) {
        return (COOR_A <= x && x <= COOR_C && y <= COOR_B);
    }
};
int main() {
    Solution sol;
    cout << sol.computeArea(-3, 0, 3, 4, 0, -1, 9, 2) << endl;
    cout << sol.computeArea(0, 0, 0, 0, -1, -1, 1, 1) << endl;
    cout << sol.computeArea(-2, -2, 2, 2, -1, -1, 1, 1) << endl;
    cout << sol.computeArea(-2, -2, 2, 2, -3, -3, -1, -1) << endl;
}
// 输出结果：
// 45
// 4
// 16
// 19

提交到 Leetcode，Accepted! :) 运行时间为 25ms。

改进

上面的代码虽然 Accepted，但实在过于繁琐，一不小心就会写错判断条件，那么有没有一个办法，可以简化判断逻辑呢？

我们先把存在重叠矩形 □MNOP 的情况列出来，看能不能找到什么规律：

(E,F) 和 (G,H) 都有可能落在区域 1～9 里：

  1. (E,F) 在区域 4，那么 (G,H) 在：
    4.2. 区域 2，形成的矩形跟 □ABCD 重叠，(M,N) = (A,F)，(O,P) = (G,D)
    4.3. 区域 3，形成的矩形跟 □ABCD 重叠，(M,N) = (A,F)，(O,P) = (C,D)
    4.5. 区域 5，形成的矩形跟 □ABCD 重叠，(M,N) = (A,F)，(O,P) = (G,H)
    4.6. 区域 6，形成的矩形跟 □ABCD 重叠，(M,N) = (A,F)，(O,P) = (C,H)
  2. (E,F) 在区域 5，那么 (G,H) 在：
    5.1. 区域 2，形成的矩形跟 □ABCD 重叠，(M,N) = (E,F)，(O,P) = (G,D)
    5.2. 区域 3，形成的矩形跟 □ABCD 重叠，(M,N) = (E,F)，(O,P) = (C,D)
    5.3. 区域 5，形成的矩形跟 □ABCD 重叠，(M,N) = (E,F)，(O,P) = (G,H)
    5.4. 区域 6，形成的矩形跟 □ABCD 重叠，(M,N) = (E,F)，(O,P) = (C,H)
  3. (E,F) 在区域 7，那么 (G,H) 在：
    7.2. 区域 2，形成的矩形跟 □ABCD 重叠，(M,N) = (A,B)，(O,P) = (G,D)
    7.3. 区域 3，形成的矩形跟 □ABCD 重叠，(M,N) = (A,B)，(O,P) = (C,D)
    7.5. 区域 5，形成的矩形跟 □ABCD 重叠，(M,N) = (A,B)，(O,P) = (G,H)
    7.6. 区域 6，形成的矩形跟 □ABCD 重叠，(M,N) = (A,B)，(O,P) = (C,H)
  4. (E,F) 在区域 8，那么 (G,H) 在：
    8.1. 区域 2，形成的矩形跟 □ABCD 重叠，(M,N) = (E,B)，(O,P) = (G,D)
    8.2. 区域 3，形成的矩形跟 □ABCD 重叠，(M,N) = (E,B)，(O,P) = (C,D)
    8.3. 区域 5，形成的矩形跟 □ABCD 重叠，(M,N) = (E,B)，(O,P) = (G,H)
    8.4. 区域 6，形成的矩形跟 □ABCD 重叠，(M,N) = (E,B)，(O,P) = (C,H)

可以看到，(E,F) 落在区域 4、5、7、8，(G,H) 落在区域 2、3、5、6，如下图：

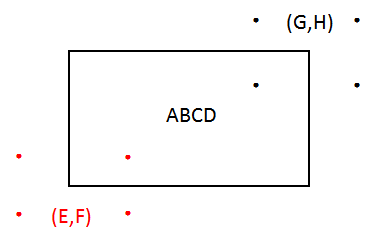
红点表示 (E,F) 所在区域，黑点表示 (G,H) 所在区域。

为了计算重叠矩形 □MNOP，我们需要计算左下角顶点 (M,N) 和右上角顶点 (O,P) 的坐标。

  • 计算 (M,N) 的 M，当 (E,F) 落在区域 4、7 时，M = A。当 (E,F) 落在区域 5、8 时，M = E。即是 M = max(A,E)。
  • 计算 (M,N) 的 N，当 (E,F) 落在区域 4、5 时，N = F。当 (E,F) 落在区域 6、7 时，M = B。即是 M = max(B,F)。
  • 计算 (O,P) 的 O，当 (G,H) 落在区域 2、5 时，O = G。当 (G,H) 落在区域 3、6 时，O = C。即是 O = min(C,G)。
  • 计算 (O,P) 的 P，当 (G,H) 落在区域 2、3 时，P = D。当 (G,H) 落在区域 5、6 时，P = H。即是 P = min(D,H)。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <frequently-used-code-snippets.h>
class Solution {
public:
    int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
        int area1 = (C - A) * (D - B);
        int area2 = (G - E) * (H - F);
        int overlapArea = computeOverlapArea2(A, B, C, D, E, F, G, H);
        return area1 + area2 - overlapArea;
    }
private:
    int computeOverlapArea2(int A, int B, int C, int D, int E, int F, int G, int H) {
        int M = MAX_TWO(A, E);
        int N = MAX_TWO(B, F);
        int O = MIN_TWO(C, G);
        int P = MIN_TWO(D, H);
        if (M <= O && N <= P) {     // 是合法矩形
            return (O - M) * (P - N);
        }
        return 0;
    }
};
int main() {
    Solution sol;
    cout << sol.computeArea(-3, 0, 3, 4, 0, -1, 9, 2) << endl;
    cout << sol.computeArea(0, 0, 0, 0, -1, -1, 1, 1) << endl;
    cout << sol.computeArea(-2, -2, 2, 2, -1, -1, 1, 1) << endl;
    cout << sol.computeArea(-2, -2, 2, 2, -3, -3, -1, -1) << endl;
}
// 输出结果：
// 45
// 4
// 16
// 19

提交到 Leetcode，Accepted! :) 运行时间为 16ms。

Leetcode 题解 - 19. Remove Nth Node From End of List
Leetcode 题解 - 290. Word Pattern