题目

给定一个非负整数 num，重复相加各位数字，直到结果只有一位数字。

示例：

给定 num = 38，执行过程：3 + 8 = 11，1 + 1 = 2，因为 2 只有一个数字，返回 2。

后续：

你的程序可以不使用任何循环/递归，且运行时间为 O(1) 吗？

难度：容易

编程语言：C++

分析

程序框架为：

class Solution {
public:
    int addDigits(int num) {
    }
};

首先，很自然的思路是，怎么取出 num 里的各位数字？如 38 怎么取出 3 和 8？

容易想到，38 / 10 = 3（int 除法），38 % 10 = 8。但对于任意 num，怎么知道 num 有多少位？

想了一下，不必知道 num 有多少位，只要按下面的方式计算即可（注意使用的除法都是 int 除法）：

38 ％ 10 ＝ 8   // 保存 8
38 / 10 = 3

3 % 10 = 3      // 保存 3
3 / 10 = 0      // 结束

再用 num = 12345 验证一下：

12345 ％ 10 ＝ 5    // 保存 5
12345 / 10 = 1234

1234 % 10 = 4       // 保存 4
1234 / 10 = 123

123 % 10 = 3        // 保存 3
123 / 10 = 12

12 % 10 = 2         // 保存 2
12 / 10 = 1

1 % 10 = 1          // 保存 1
1 / 10 = 0          // 结束

解决了分解 num 的问题后，我们再回来看看源问题的解决过程。

38 -> 3 + 8 = 11 -> 11
11 -> 1 + 1 = 2  -> 2
2  -> 结束程序

可以看到，纵向形成一个循环，即 38 -> 11 -> 2。循环结束的条件是：num 只有一位数字。

横向也形成一个循环，即 3 + 8 = 11，或 1 + 1 = 2，循环结束的条件是：num 分解后的各位数字全部相加完毕。

写法一：循环

根据上面的思路，我们可以写出两个嵌套的循环，伪代码如下：

int addDigits(int num)
    temp = num
    while (true)    // 纵循环
        if (getNumDigits(temp) == 1)
            return temp
    
        temp = 0
        for (each digit in num)     // 横循环
            temp += digit

getNumDigits 函数，输入为 int num，输出为 int numDigits。方法就是上面提到的分解 num 的方法。我们把每位数字保存到一个 vector 里。那么 getNumDigits 的输入修改为 int num 和 vector&。

int addDigits(int num, vector<int>& vecDigits)
    temp = num
    while (true)    // 纵循环
        numDigits = getNumDigits(temp, vecDigits)
        if (numDigits == 1)
            return temp
    
        temp = 0
        for (each digit in vecDigits)     // 横循环
            temp += digit
        reset vector

我们再编写 getNumDigits 的伪代码：

int getNumDigits(int num, vector<int>& vecDigits)
    vecDigits.clear()
    while (true)
        if (num == 0)
            return vector.size()
        int lastDigit = num % 10
        vector.add(lastDigit)
        num /= 10

全部代码如下：

#include <iostream>
#include<vector>
using namespace std;
class Solution {
public:
    int addDigits(int num) {
        int temp = num;
        vector<int> vecDigits;
        while (true) {
            // calculate number of digits of num
            int numDigits = getNumDigits(temp, vecDigits);
            // end function
            if (numDigits == 1) {
                // TODO: release vector memory
                return temp;
            }
            // repeatedly add all num's digits
            temp = 0;
            for (int digit : vecDigits) {
                temp += digit;
            }
            // reset vector
            vecDigits.clear();
        }
    }
    
    int getNumDigits(int num, vector<int>& vecDigits) {
        vecDigits.clear();
        while (true) {
            if (num == 0) {
                return vecDigits.size();
            }
            int lastDigis = num % 10;
            vecDigits.push_back(lastDigis);
            num /= 10;
        }
    }
};
int main() {
    Solution sol;
    int result = sol.addDigits(100);
    cout << result << endl;
}

运行结果：

输入 38，输出 2，正确
输入 12345，输出 6，正确

提交到 Solution 到 Leetcode，Time Limit Exceeded（下面简称 TLE），为什么？哪里耗时多了？

用 VS2013 Performance Wizard 分析了程序的运行时间，见下图：

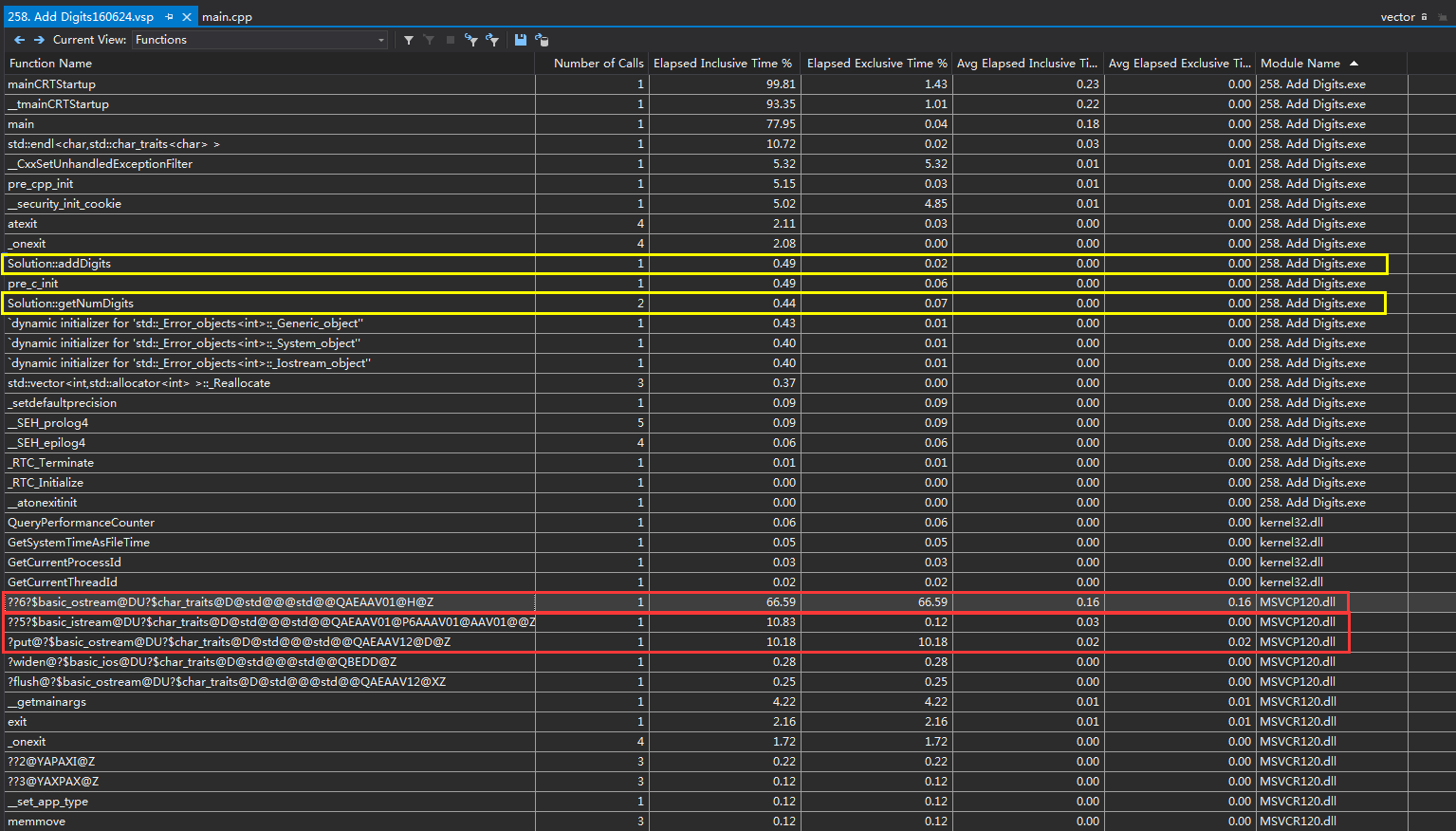
其中，黄色框是我编写的函数，红色框是耗时比较多的函数。可以看到在 Elapsed Inclusive Time 里：

 0.49%  |   addDigits
 0.44%  |   getNumDigits
66.59%  |   ??6?$basic_ostream@DU?$char_traits@D@std@@@std@@QAEAAV01@H@Z
10.83%  |   ??5?$basic_istream@DU?$char_traits@D@std@@@std@@QAEAAV01@P6AAAV01@AAV01@@Z@Z
10.18%  |   ?put@?$basic_ostream@DU?$char_traits@D@std@@@std@@QAEAAV12@D@Z

如果不使用 vector，把 num 分解后直接相加各位数字，能避免 TLE 吗？

我们回看分析过程：

38 -> 3 + 8 = 11 -> 11
11 -> 1 + 1 = 2  -> 2
2  -> 结束程序

纵循环：38 -> 11 -> 2
横循环：3 + 8

在把 38 分解出 3、8 之后，就不使用 vector 保存各位数字了，每分解出一位，就加一位。伪代码如下：

int addDigits(int num)
    while (num / 10 > 0)     // 纵循环
        int temp = num
        int sum = 0
        while (temp > 0)     // 横循环
            int lastDigit = temp % 10
            sum += lastDigit
            temp /= 10
        // 更新 num
        num = sum
    return num

代码如下：

class Solution {
public:
    int addDigits(int num) {
        while (num / 10 > 0) {      // 纵循环
            int temp = num;
            int sum = 0;
            while (temp > 0) {      // 横循环
                int lastDigit = temp % 10;
                sum += lastDigit;
                temp /= 10;
            }
            num = sum;
        }
        return num;
    }
};

提交到 Leetcode，Accepted! :) 运行时间为 8ms。

写法二：递归

我们再使用递归来改写一下程序，回看分析过程：

38 -> 3 + 8 = 11 -> 11
11 -> 1 + 1 = 2  -> 2
2  -> 结束程序

纵循环：38 -> 11 -> 2
横循环：3 + 8

再回看 addDigits 函数签名：

int addDigits(int num)

容易想到，首先调用 addDigits(38)，把 38 处理为 11 后，尾递归调用 addDigits(11)，把 11 处理为 2 后，尾递归调用 addDigits(2)，而递归的结束条件（base case）则是 num / 10 == 0。伪代码如下：

int addDigits(int num)
    // 递归结束条件
    if (num / 10 == 0)
        return num
    int sum = 0
    while (num > 0)     // 横循环
        int lastDigit = num % 10
        sum += lastDigit
        num /= 10
    
    // 递归（即纵循环）
    return addDigits(sum)

代码如下：

class Solution {
public:
    int addDigits(int num) {
        // 递归结束条件
        if (num / 10 == 0) {
            return num;
        }
        int sum = 0;
        while (num > 0) {   // 横循环
            int lastDigit = num % 10;
            sum += lastDigit;
            num /= 10;
        }
        // 递归（即纵循环）
        return addDigits(sum);
    }
};

提交到 Leetcode，Accepted! :) 运行时间为 12ms。

写法三：O(1)

题目的后续：

你的程序可以不使用任何循环/递归，且运行时间为 O(1) 吗？

回看 38 和 12345 的分解过程，看能不能找到什么规律。

38 -> 3 + 8 = 11 -> 11
11 -> 1 + 1 = 2  -> 2
2  -> 结束程序

12345 -> 1 + 2 + 3 + 4 + 5 = 15
15 -> 1 + 5 = 6
6  -> 结束程序

我们干脆从 1 开始，看所有 num 的 addDigits(num) 有什么规律：

规律很明显：addDigits(num) 的结果以 9 为一个循环，代码就很好写了：

class Solution {
public:
    int addDigits4(int num) {
        int result = (num - 1) % 9 + 1;
        return result;
    }
}

提交到 Leetcode，Accepted! :) 运行时间为 12ms。

syawlaus

Leetcode 题解 - 258. Add Digits

题目

分析

写法一：循环

写法二：递归

写法三：O(1)